已知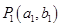 是曲线C:
是曲线C: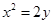 上的一点(其中
上的一点(其中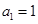 ),过点
),过点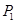 作与曲线C在
作与曲线C在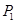 处的切线垂直的直线
处的切线垂直的直线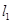 交
交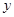 轴于点
轴于点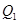 ,过
,过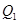 作与
作与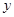 轴垂直的直线
轴垂直的直线 与曲线C在第一象限交于点
与曲线C在第一象限交于点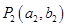 ;再过点
;再过点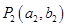 作与曲线C在
作与曲线C在 处的切线垂直的直线
处的切线垂直的直线 交轴于点
交轴于点 ,过
,过 作与
作与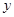 轴垂直的直线
轴垂直的直线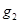 与曲线C在第一象限交于点
与曲线C在第一象限交于点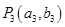 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点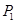 、
、 、、
、、 、。(其中
、。(其中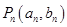 )
)
(1)求数列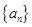 的通项公式。
的通项公式。
(2)若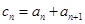 ,且
,且 是数列
是数列 的前
的前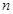 项和,
项和, 是数列
是数列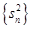 的前
的前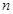 项
项
如图,在三棱锥P -ABC中,点P在平面ABC上的射影D是AC的中点.BC ="2AC=8,AB" =

(I )证明:平面PBC丄平面PAC
(II)若PD = ,求二面角A-PB-C的平面角的余弦值.
,求二面角A-PB-C的平面角的余弦值.
某大学体育学院在2012年新招的大一学生中,随机抽取了 40名男生,他们的身高(单位:cm)情况共分成五组:第1组[175,180),第 2 组[180,185),第 3 组 [185,190),第 4 组[190,195),第 5 组[195,200) .得到的频率分布直方图(局部)如图所示,同时规定身高在185cm以上(含185cm)的学生成为组建该校篮球队的“预备生”.
(I)求第四组的频率并补布直方图;
(II)如果用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
(III)若该校决定在第4,5组中随机抽取2名学生接受技能测试,第5组中有ζ名学生接受测试,试求ζ的分布列和数学期望.
已ΔABC的内角A,B,C对的边分别为a,b,c =" (2a,C" -26) ,
=" (2a,C" -26) ,  = (cosC,l),且
= (cosC,l),且 丄
丄 .
.
(I)求角A的大小;
(II )若a = 1,求b +c的取值范围.
已知函数 .
.
(I)证明: ;
;
(II)求不等式 的解集.
的解集.
在直接坐标系 中,直线
中,直线 的方程为
的方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数)
为参数)
(I)已知在极坐标(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4, ),判断点
),判断点 与直线
与直线 的位置关系;
的位置关系;
(II)设点 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.