(1)如图,在Rt△ABC中,∠C=90°,AC=BC,小明为了求tan67.5°值,他延长CB到D,使BD=BA,连接AD,请你根据图形计算tan67.5°;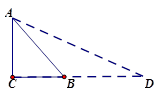
(2)请你仿照小明的方法构造图形求tan75°.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,CD与AB的延长线相交于点E,∠ADC=60°.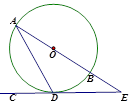
(1)求证:△ADE是等腰三角形;
(2)若AD=2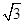 ,求BE的长.
,求BE的长.
已知,如图,点B、C、D在⊙O上,四边形OCBD是平行四边形,
(1)求证:
(2)若⊙O的半径为2,求 的长.
的长.
某工厂甲、乙两名工人参加操作技能培训.现分别从他们若干次测试成绩中随机抽取5次,记录如下:
| 次数 |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
平均数 |
中位数 |
|
| 甲 |
87 |
91 |
94 |
90 |
88 |
|||
| 乙 |
91 |
89 |
92 |
86 |
92 |
(1)请你计算两组数据的平均数、中位数,并把求得的结果填入表格中;
(2)分别计算甲、乙两名工人五次测试成绩的方差;
(3)现要从中选派一人参加操作技能比赛,你认为选派哪名工人参加合适?请说明理由.
已知关于x的方程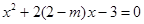 ,
,
(1)若x=1是此方程的一根,求m的值及方程的另一根;
(2)证明:无论m取什么实数值,此方程总有实数根.