在平面直角坐标系xOy中,已知二次函数 的图像经过原点及点A(1,2),与x轴相交于另一点B.
的图像经过原点及点A(1,2),与x轴相交于另一点B.
(1)求:二次函数 的解析式及B点坐标;
的解析式及B点坐标;
(2)若将抛物线 以
以 为对称轴向右翻折后,得到一个新的二次函数
为对称轴向右翻折后,得到一个新的二次函数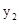 ,已知二次函数
,已知二次函数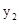 与x轴交于两点,其中右边的交点为C点.点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D.点E、点F也随之运动);
与x轴交于两点,其中右边的交点为C点.点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D.点E、点F也随之运动);
①当点E在二次函数y1的图像上时,求OP的长.
②若点P从O点出发向C点做匀速运动,速度为每秒1个单位长度,同时线段OC上另一个点Q从C点出发向O点做匀速运动,速度为每秒2个单位长度(当Q点到达O点时停止运动,P点也同时停止运动).过Q点作x轴的垂线,与直线AC交于G点,以QG为边在QG的左侧作正方形QGMN(当Q点运动时,点G、点M、点N也随之运动),若P点运动t秒时,两个正方形分别有一条边恰好落在同一条直线上(正方形在x轴上的边除外),求此刻t的值.
已知:如图,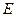 、
、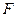 在
在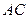 上,
上,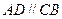 且
且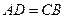 ,
,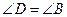 .
.
求证:
甲、乙两厂生产同一种产品,都计划把全年的产品销往重庆,这样两厂的产品就能占有重庆市场同类产品的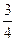 .然而实际情况并不理想,甲厂仅有
.然而实际情况并不理想,甲厂仅有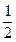 的产品、乙厂仅有
的产品、乙厂仅有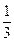 的产品销到了重庆,两厂的产品仅占了重庆市场同类产品的
的产品销到了重庆,两厂的产品仅占了重庆市场同类产品的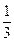 .则甲厂该产品的年产量与乙厂该产品的年产量的比为.
.则甲厂该产品的年产量与乙厂该产品的年产量的比为.
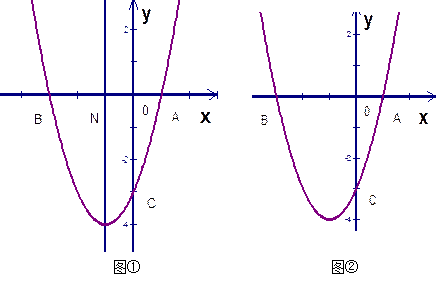
如图①, 已知抛物线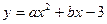 (a≠0)与
(a≠0)与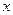 轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) 求抛物线的解析式;
轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) 求抛物线的解析式;
(2) 设抛物线的对称轴与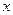 轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
轴交于点N ,问在对称轴上是否存在点P,使△CNP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3) 如图②,若点E为第三象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
 |
已知二次函数y=x2-2x-3.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)画出此抛物线图象;
(3)利用图象回答下列问题:
①方程x2-2x-3=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
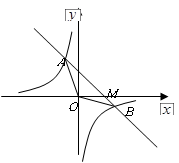
如图,已知一次函数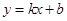 的图象与反比例函数
的图象与反比例函数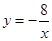 的图
的图
象交于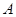 ,
,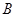 两点,且点
两点,且点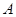 的横坐标和
的横坐标和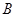 点的纵坐标都是
点的纵坐标都是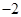 .求:
.求:
(1)一次函数解析式;
(2)求 的面积.
的面积.
(3)观察图像,直接写出一次函数值小于反比例函数值的x的取值范围
 |