已知曲线C的极坐标方程为 ,直线
,直线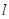 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤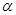 <
< ).
).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线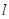 经过点(1,0),求直线
经过点(1,0),求直线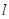 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
已知下列三个方程: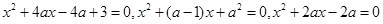 至少有一个方程有实数根.求实数
至少有一个方程有实数根.求实数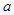 的取值范围.
的取值范围.
设命题p:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
如图已知抛物线 :
: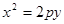 过点
过点 ,直线
,直线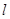 交
交 于
于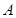 ,
,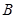 两点,过点
两点,过点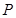 且平行于
且平行于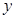 轴的直线分别与直线
轴的直线分别与直线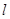 和
和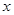 轴相交于点
轴相交于点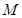 ,
,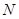 .
.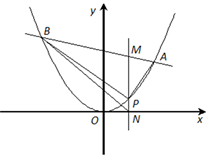
(1)求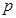 的值;
的值;
(2)是否存在定点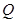 ,当直线
,当直线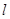 过点
过点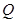 时,△
时,△ 与△
与△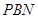 的面积相等?若存在,求出点
的面积相等?若存在,求出点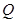 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
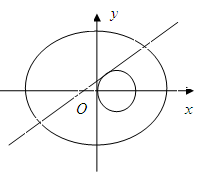
已知中心在坐标原点,焦点在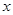 轴上的椭圆过点
轴上的椭圆过点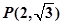 ,且它的离心率
,且它的离心率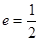 .
.
(1)求椭圆的标准方程;
(2)与圆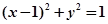 相切的直线
相切的直线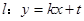 交椭圆于
交椭圆于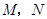 两点,若椭圆上一点
两点,若椭圆上一点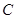 满足
满足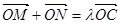 ,求实数
,求实数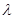 的取值范围.
的取值范围.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.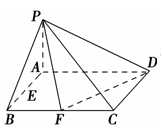
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.