某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表: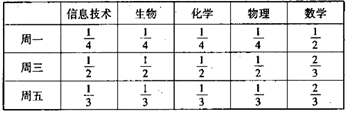
根据上表:
(Ⅰ)求数学辅导讲座在周一、周三、周五都不满座的概率;
(Ⅱ)设周三各辅导讲座满座的科目数为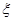 ,求随机变量
,求随机变量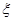 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)调查表明,中年人的成就感与收入、学历、职业的满意度的指标有极强的相关性.现将这三项的满意度指标分别记为 ,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标
,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标 的值评定中年人的成就感等级:若
的值评定中年人的成就感等级:若 ,则成就感为一级;若
,则成就感为一级;若 ,则成就感为二级;若
,则成就感为二级;若 ,则成就感为三级.为了了解目前某群体中年人的成就感情况,研究人员随机采访了该群体的10名中年人,得到如下结果:
,则成就感为三级.为了了解目前某群体中年人的成就感情况,研究人员随机采访了该群体的10名中年人,得到如下结果:
| 人员编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 人员编号 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(Ⅰ)在这10名被采访者中任取两人,求这两人的职业满意度指标 相同的概率;
相同的概率;
(Ⅱ)从成就感等级是一级的被采访者中任取一人,其综合指标为 ,从成就感等
,从成就感等
级不是一级的被采访者中任取一人,其综合指标为 ,记随机变量
,记随机变量 ,求
,求 的分布列及其数学期望.
的分布列及其数学期望.
(本小题满分12分)已知函数 的图象与直线
的图象与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)设 的内角
的内角 所对的边分别是
所对的边分别是 .若
.若
 ,求角
,求角 的大小.
的大小.
(本小题满分14分)已知函数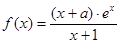 (
(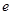 为自然对数的底数),曲线
为自然对数的底数),曲线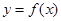 在
在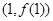 处的切线与直线
处的切线与直线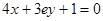 互相垂直.
互相垂直.
(Ⅰ)求实数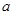 的值;
的值;
(Ⅱ)若对任意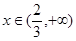 ,
, 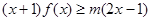 恒成立,求实数
恒成立,求实数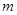 的取值范围;
的取值范围;
(Ⅲ)设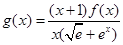 ,
,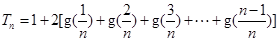
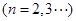 .问:是否存在正常数
.问:是否存在正常数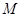 ,对任意给定的正整数
,对任意给定的正整数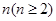 ,都有
,都有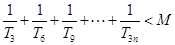 成立?若存在,求
成立?若存在,求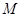 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(本小题满分13分)如图,已知椭圆 的离心率为
的离心率为 ,其左、右顶点分别为
,其左、右顶点分别为 .一条不经过原点的直线
.一条不经过原点的直线 与该椭圆相交于
与该椭圆相交于 、
、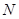 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若 ,直线
,直线 与
与 的斜率分别为
的斜率分别为 .试问:是否存在实数
.试问:是否存在实数 ,使得
,使得 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)已知等差数列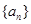 单调递增,且
单调递增,且 ,
, 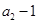 是
是 与
与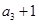 的等比中项.
的等比中项.
(Ⅰ)求数列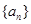 的通项公式;
的通项公式;
(Ⅱ)设数列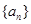 的前
的前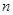 项和为
项和为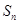 ,求数列
,求数列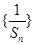 的前
的前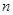 项和
项和 .
.