设椭圆 的左、右顶点分别为
的左、右顶点分别为 、
、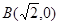 ,离心率
,离心率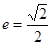 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且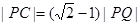 .
.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线MN过椭圆的右焦点与椭圆相交于M、N两点,且 ,求直线MN的方程.
,求直线MN的方程.
(本小题满分12分)如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB的中点.
(1)求证:AC1∥平面CNB1;
(2)求四棱锥C-ANB1A1的体积.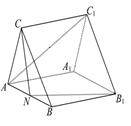
(本小题满分12分)分别用二种方法写出算法语句,计算:1+2+3+……+99+100.
(本小题满分12分)已知函数f(x)=(x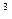 +3x
+3x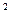 +ax+b)e
+ax+b)e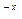 。
。
(1) 若a =" b" =  3 ,求f (x) 的单调区间;
3 ,求f (x) 的单调区间;
(2) 若f (x) 在( ,
, ),(2,
),(2, )上单调递增,在(
)上单调递增,在( ,2),(
,2),( ,+
,+ )上单调递减,证明:
)上单调递减,证明: -
- >6。
>6。
(本小题满分12分)设等差数列{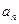 }的前n项和为
}的前n项和为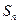 ,且
,且 。
。
(1)求数列{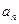 }的通项公式及前n项和公式;
}的通项公式及前n项和公式;
(2)设数列{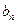 }的通项公式为
}的通项公式为 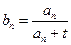 ,是否存在正整数t,使得
,是否存在正整数t,使得 成等差数列?若存在,求出t和m的值;若不存在,请说明理由
成等差数列?若存在,求出t和m的值;若不存在,请说明理由
(本小题满分12分)设数列{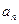 }满足
}满足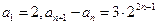 。
。
(1)求数列{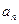 }的通项公式;
}的通项公式;
(2)令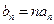 ,求数列{
,求数列{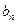 }的前n项和
}的前n项和 。
。