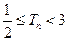某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。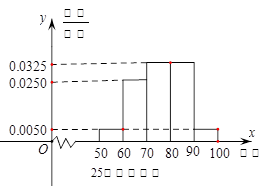
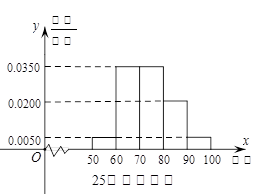
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
(本小题满分12分)
定义在非零实数集上的函数 满足关系式
满足关系式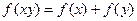 且
且 在区间
在区间 上是增函数
上是增函数
(1)判断函数 的奇偶性并证明你的结论;
的奇偶性并证明你的结论;
(2)解不等式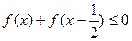
(本小题满分12分)
已知锐角△ABC的三内角A、B、C的对边分别是a、b、c,且(b2+c2-a2)tanA=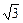 bc.
bc.
(1)求角A的大小;
(2)求sin(A+10°)·[1-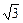 tan(A-10°)]的值.
tan(A-10°)]的值.
(本小题满分12分)
已知向量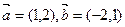 ,
,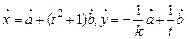 ,k,t为实数.
,k,t为实数.
(Ⅰ)当k=-2时,求使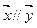 成立的实数t值;
成立的实数t值;
(Ⅱ)若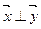 ,求k的取值范围.
,求k的取值范围.
(本小题满分13分)
已知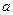 是实数,设函数
是实数,设函数
(1)讨论函数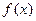 的单调性;
的单调性;
(2)设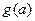 为函数
为函数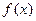 在区间
在区间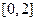 上的最小值
上的最小值
① 写出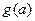 的表达式;
的表达式;
② 求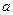 的取值范围,使得
的取值范围,使得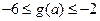
、(本小题满分13分)
已知等差数列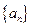 中,
中,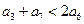 且
且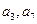 是方程
是方程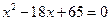 的两根,数列
的两根,数列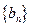 的前项和
的前项和 .
.
(1)求数列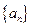 和
和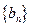 的通项公式;
的通项公式;
(2)记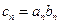 ,求数列
,求数列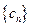 的前
的前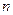 项的和
项的和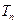 ,并证明
,并证明