为了解“校本课程”开展情况,某校科研室随机选取了若干学生进行问卷调查(要求每位学生只能填写一种自己喜欢的课程),并将调查的结果绘制成如下两幅不完整的统计图:
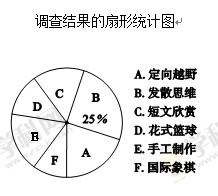
请根据以上信息回答下列问题:
(1)参加问卷调查的学生共有 人;
(2)在扇形统计图中,表示“C”的扇形的圆心角为 度;
(3)统计发现,填写“喜欢手工制作”的学生中,男生人数∶女生人数=1∶6.如果从所有参加问卷调查的学生中随机选取一名学生,那么这名学生是填写“喜欢手工制作”的女生的概率为 .
我们知道,经过原点的抛物线解析式可以是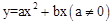 。
。
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a=;
当顶点坐标为(m,m),m≠0时,a 与m之间的关系式是;
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线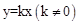 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;
(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线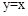 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
如图,等腰梯形ABCD中,AD∥BC,∠B=450,P是BC边上一点,△PAD的面积为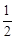 ,设AB=x,AD=y。
,设AB=x,AD=y。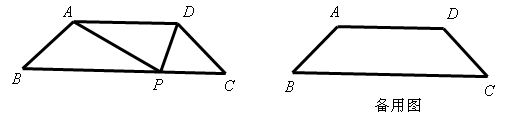
(1)求y与x的函数关系式;
(2)若∠APD=450,当y=1时,求PB·PC的值;
(3)若∠APD=900,求y的最小值。
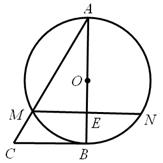
如图,△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE= 。
。
(1)求证:BC是⊙O的切线;
(2)求 的长。
的长。
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。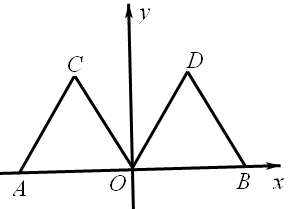
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△OBD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是度;
(2)连接AD,交OC于点E,求∠AEO的度数。
为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查。已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计图表:
根据图表提供的信息,回答下列下列问题:
(1)样本中,男生身高的众数在组,中位数在组;
(2)样本中,女生身高在E组的人数有人;
(3)已知该校共有男生400人,女生380人,请估计身高在 之间的学生约有多少人?
之间的学生约有多少人?