已知椭圆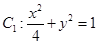 ,椭圆
,椭圆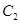 以
以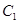 的长轴为短轴,且与
的长轴为短轴,且与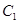 有相同的离心率.
有相同的离心率.
(1)求椭圆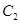 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆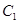 和
和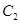 上,
上, 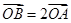 ,求直线
,求直线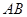 的方程.
的方程.
(本小题满分12分)如图,斜三棱柱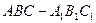 ,已知侧面
,已知侧面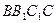 与底面ABC垂直且∠BCA =90°,∠
与底面ABC垂直且∠BCA =90°,∠ ,
, =2,若二面角
=2,若二面角 为30°.(Ⅰ)证明
为30°.(Ⅰ)证明 ;
; 
(Ⅱ)求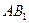 与平面
与平面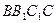 所成角的正切值;
所成角的正切值;
(Ⅲ)在平面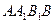 内找一点P,使三棱锥
内找一点P,使三棱锥 为正三棱锥,并求P到平面
为正三棱锥,并求P到平面 距离.
距离.
(本小题满分12分)在△OAB的边OA、OB上分别有一点P、Q,已知 :
: =1:2,
=1:2, 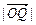 :
: =3:2,连结AQ、BP,设它们交于点R,若
=3:2,连结AQ、BP,设它们交于点R,若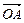 =a,
=a, =b.(Ⅰ)用a与 b表示
=b.(Ⅰ)用a与 b表示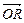 ;
;
(Ⅱ)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角 的范围.
的范围.
(本小题满分10分)如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为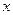 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为 ,
,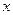 、
、

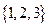 ,设
,设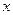 +
+ 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
.
(Ⅰ)求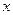 <2且
<2且 >1的概率;
>1的概率;
(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.
(本小题满分13分)已知点A是抛物线y2=2px(p>0)上一点,F为抛物线的焦点,准线l与x轴交于点K,已知|AK|= |AF|,三角形AFK的面积等于8. (Ⅰ)求p的值;(Ⅱ)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦的中点分别为G,H.求|GH|的最小值.
|AF|,三角形AFK的面积等于8. (Ⅰ)求p的值;(Ⅱ)过该抛物线的焦点作两条互相垂直的直线l1,l2,与抛物线相交得两条弦,两条弦的中点分别为G,H.求|GH|的最小值.
(本小题满分12分)设函数f(x)=(x+2)2-2ln(x+2). (Ⅰ)求f(x)的单调区间;(Ⅱ)若关于x的方程f(x)=x2+3x+a在区间[-1,1]上只有一个实数根,求实数a的取值范围.