如图,已知圆 与圆
与圆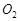 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于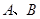 两点,
两点, 是圆
是圆 的直径,过
的直径,过 作圆
作圆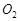 的切线,切点为
的切线,切点为 .
.
(Ⅰ)求证: 三点共线;
三点共线;
(Ⅱ)求证: .
.
(本小题满分12分)
已知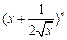 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值; (2)求展开式中系数最大的项.
(2)求展开式中系数最大的项.
(本小题满分12分)已知向量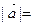 (
( )和
)和 (
(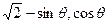 ),
), .
.
(1)求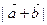 的最大值;(2)若
的最大值;(2)若
 ,求
,求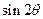 的值
的值 .
.
(本小题满分14分)在直角坐标系xoy中,已知三点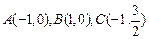
以A、B为焦点的椭圆经过C点,
(1) 求椭圆方程;
(2) 设点D(0,1),是否存在不平行于x轴的直线l,与椭圆交于不同的两点M、N,使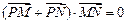 ?
?
若存在。求出直线l斜率的取值范围;
⑶对于y轴上的点P(0,n)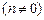 ,存在不平行于x轴的直线l与椭圆交于不同两点M、N,使
,存在不平行于x轴的直线l与椭圆交于不同两点M、N,使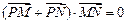 ,试求实数n的取值范围。
,试求实数n的取值范围。
(本小题满分12分)如图,AB为圆O的直
径,点E、F在圆O上,AB∥EF,矩形ABCD
所在的平面和圆O所在的平面垂直,且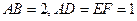 .
.
⑴求证: ;
;
⑵设FC的中点为M,求证: ;
;
⑶设平面CBF将 几何体分成的两个锥体的体积分别为
几何体分成的两个锥体的体积分别为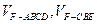 ,求
,求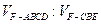 的值.
的值.
(本小题满分12分)在平面上给定非零向量 满足
满足 ,
, 的夹角为600,
的夹角为600,
(1) 试计算 和
和 的值;
的值;
(2) 若向量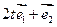 与向量
与向量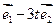 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.