如图所示,点O、B坐标分别为(0,0)、(3,0),将△ABO绕点O按逆时针方向旋转90°得到△OA'B';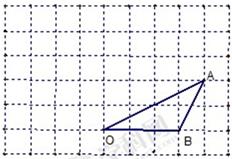
⑴根据题中条件在图中画出直角坐标系,并画出△OA′B′;
⑵点A′的坐标是 ;
⑶求BB′的长;
“农民也可以报销医疗费了!”这是我区推行新型农村医疗合作的成果。村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款,这一举措极大地增强了农民抵御大病风险的能力。小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图。根据以上信息,解答以下问题:
(1)本次调查了多少村民?被调查的村民中,有多少人参加合作医疗得到了返回款?
(2)该乡若有10000村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年增长率相同,求这个年增长率。
如图21,AB为⊙O的直径,弦CD⊥AB于点M,过点B做BE∥CD,交AC的延长线于点E,连结AD。
(1)求证:BE为⊙O的切线;
(2)如果CD=8, ,求⊙O的直径。
,求⊙O的直径。
现要建造一段水坝,它的横截面是梯形ABCD,其上底CD=4米,斜坡BC的坡度 ,
, ,坝高DE=6米.
,坝高DE=6米.
(1)求截面梯形的面积;
(2)若该水坝的长为1000米,工程由甲、乙两个工程队同时合作完成,原计划需要25天,但在开工时,甲工程队增加了机器,工作效率提高60%,结果工程提前了5天完成,问这两个工程队原计划每天各完成多少土方?(坝的土方=坝的横截面的面积×坝的长度)
“五一”期间,广州市先后有两批游客分别乘中巴车和小轿车沿相同路线从广州市赶往汕头市澄海区旅游,如图表示其行驶过程中路程随时间的变化图象.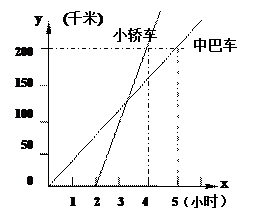
(1)根据图象,请分别直接写出中巴车和小轿车行驶过程中路程与时间之间的函数关系式(不要求写自变量的取值范围);
(2)直接写出中巴车和小轿车行驶速度各是多少?
(3)试求小轿车出发后多长时间赶上中巴车?
路边有一根电线杆AB和一块正方形广告牌.有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,正方形边长为3米,DE=4米.
(1)求电线杆落在广告牌上的影长;
(2)求电线杆的高度(精确到0.1米).