路边有一根电线杆AB和一块正方形广告牌.有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,正方形边长为3米,DE=4米.
(1)求电线杆落在广告牌上的影长;
(2)求电线杆的高度(精确到0.1米).
如图,矩形 的对角线 , 相交于点 ,点 , 在 上, .
(1)求证: ;
(2)若 , ,求矩形 的面积.

如图,在平面直角坐标系中, 的三个顶点分别为 , , .
(1)把 向上平移3个单位后得到△ ,请画出△ 并写出点 的坐标;
(2)已知点 与点 关于直线 成轴对称,请画出直线 及 关于直线 对称的△ ,并直接写出直线 的函数解析式.

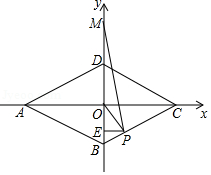
以菱形 的对角线交点 为坐标原点, 所在的直线为 轴,已知 , , , 为折线 上一动点,作 轴于点 ,设点 的纵坐标为 .
(1)求 边所在直线的解析式;
(2)设 ,求 关于 的函数关系式;
(3)当 为直角三角形时,求点 的坐标.
已知 的内切圆 与 、 、 分别相切于点 、 、 ,若 ,如图1.
(1)判断 的形状,并证明你的结论;
(2)设 与 相交于点 ,如图2, ,求 的长.

某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从 开始, 之前演出结束,问参与的小品类节目最多能有多少个?