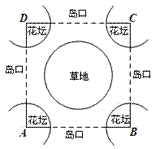
如图,现要在边长为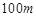 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为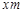 (
(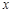 不小于
不小于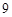 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为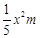 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于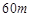 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于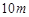 .
.
(1)求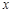 的取值范围;(运算中
的取值范围;(运算中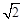 取
取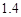 )
)
(2)若中间草地的造价为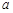 元
元 ,四个花坛的造价为
,四个花坛的造价为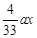 元
元 ,其余区域的造价为
,其余区域的造价为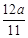 元
元 ,当
,当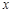 取何值时,可使“环岛”的整体造价最低?
取何值时,可使“环岛”的整体造价最低?
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a, ,种草的面积为
,种草的面积为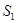 ,种花的面积为
,种花的面积为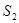 ,比值
,比值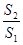 称为“规划和谐度”。
称为“规划和谐度”。
(I)试用 表示
表示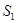 ,
,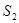 ;
;
(II)若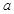 为定值,BC >AB。当
为定值,BC >AB。当 为何值时,“规划和谐度”有最小值?最小值是多少?
为何值时,“规划和谐度”有最小值?最小值是多少?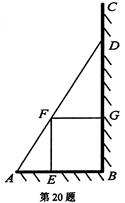
已知函数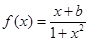 为奇函数。
为奇函数。
(I)证明:函数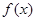 在区间(1,
在区间(1, )上是减函数;
)上是减函数;
(II)解关于x的不等式
已知函数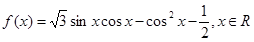
(I)求函数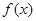 的最小值和最小正周期;
的最小值和最小正周期;
(II)已知△ABC内角A,B,C的对边分别为a,b,c,且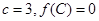 ,若向量
,若向量 共线,求a,b的值。
共线,求a,b的值。
已知数列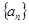 满足:
满足: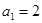 ,
,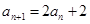 。
。
(I)求证:数列 是等比数列(要求指出首项与公比);
是等比数列(要求指出首项与公比);
(II)求数列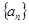 的前n项和
的前n项和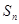 。
。
(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.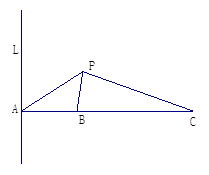
(1)设A到P的距离为 km,用
km,用 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求 值;
值;
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)