生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为
次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |
 |
 |
 |
 |
 |
| 元件A |
8 |
12 |
40 |
32 |
8 |
| 元件B |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计元件A、元件B为正品的概率;
(Ⅱ)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
设命题 :函数
:函数 在
在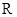 上是增函数,命题
上是增函数,命题 :
:
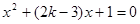 ,如果
,如果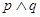 是假命题,
是假命题,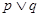 是真命题,求
是真命题,求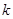 的取值范围.
的取值范围.
已知集合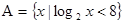 ,
, ,
,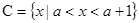 .
.
(Ⅰ)求集合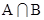 ;
;
(Ⅱ)若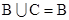 ,求实数
,求实数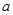 的取值范围.
的取值范围.
设 ,函数
,函数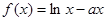 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)设 问
问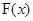 是否存在极值,若存在,请求出极值;若不存在,请说明理由;
是否存在极值,若存在,请求出极值;若不存在,请说明理由;
(Ⅲ)设 是函数
是函数 图象上任意不同的两点,线段
图象上任意不同的两点,线段 的中点为
的中点为 直线
直线 的斜率为
的斜率为 .证明:
.证明: .
.
某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度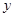 (单位:毫克/立方米)随着时间
(单位:毫克/立方米)随着时间 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为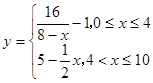 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求 的最小值(精确到
的最小值(精确到 ,参考数据:
,参考数据: 取
取 ).
).
已知二次函数 .
.
(Ⅰ)若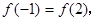 且函数
且函数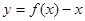 的值域为
的值域为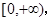 求函数
求函数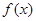 的解析式;
的解析式;
(Ⅱ)若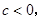 且函数
且函数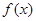 在
在 上有两个零点,求
上有两个零点,求 的取值范围.
的取值范围.