由某种设备的使用年限 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得 ,
, ,
, ,
,  .
.
(Ⅰ)求所支出的维修费 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中 ,
, 为
为
样本平均值,线性回归方程也可写为 .
.
(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2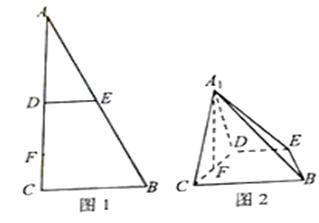
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
(本小题共13分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(1)求上图中 的值;
的值;
(2)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(3)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明)
(本小题共13分)已知函数 ,
,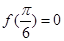
(1)求实数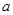 的值;
的值;
(2)求函数 的最小正周期及单调增区间.
的最小正周期及单调增区间.
(本小题共13分)已知在等比数列 中,
中, ,且
,且 是
是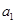 和
和 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求
,求 的前
的前 项和
项和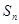 .
.
(本小题共15分)已知函数 对任意实数
对任意实数 恒有
恒有 且当x>0,
且当x>0,
(1)判断 的奇偶性;
的奇偶性;
(2)求 在区间[-3,3]上的最大值;
在区间[-3,3]上的最大值;
(3)解关于 的不等式
的不等式