(本小题满分12分)已知曲线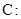
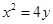 .
.
(1)若 ,
,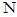 为曲线
为曲线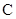 上两点,且
上两点,且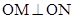 ,求
,求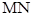 的中点轨迹方程;
的中点轨迹方程;
(2)过曲线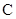 的焦点
的焦点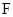 作直线
作直线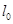 交曲线
交曲线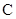 于
于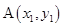 、
、 ,其中
,其中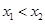 ,分别作在点
,分别作在点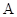 、
、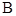 处的切线
处的切线 、
、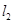 ,若动点
,若动点 (
( )在曲线
)在曲线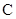 上,曲线
上,曲线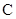 在点
在点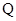 处的切线
处的切线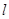 交
交 、
、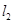 于点
于点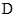 、
、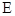 ,求证:
,求证: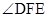 为定值.
为定值.
(本小题满分12分)一个盒子中装有大小相同的小球 个,在小球上分别标有
个,在小球上分别标有 ,
, ,
, ,
, ,
, 的号码,已知从盒子中随机地取出
的号码,已知从盒子中随机地取出 个球,
个球, 个球的号码最大值为
个球的号码最大值为 的概率为
的概率为 .
.
(1)求 的值;
的值;
(2)现从盒子中随机地取出 个球,记所取
个球,记所取 个球的号码中,连续自然数的个数的最大值为随机变量
个球的号码中,连续自然数的个数的最大值为随机变量 (如取
(如取 时,
时, ;取
;取 时,或取
时,或取 时,
时, ;取
;取 时,
时, ).
). 求
求 的值;
的值; 求随机变量
求随机变量 的分布列及期望.
的分布列及期望.
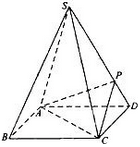
(本小题满分12分)如图,正四棱锥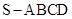 中,
中,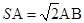 .
.
(1)求证: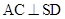 ;
;
(2)在线段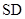 上是否存在点
上是否存在点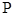 ,使得二面角
,使得二面角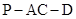 的大小为
的大小为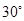 ,若存在,求出
,若存在,求出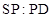 ;若不存在,试说明理由.
;若不存在,试说明理由.
(本小题满分12分) 中内角
中内角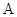 、
、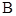 、
、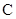 的对边分别为
的对边分别为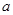 、
、 、
、 ,
,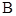 为锐角,向量
为锐角,向量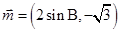 ,
,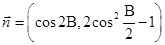 ,且
,且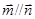 .
.
(1)求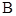 的大小;
的大小;
(2)若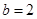 ,求
,求 的最大值.
的最大值.
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(Ⅰ)解不等式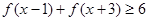 ;
;
(Ⅱ)若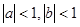 ,且
,且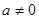 ,求证:
,求证: .
.