已知平面内两点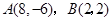 .
.
(1)求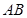 的中垂线方程;
的中垂线方程;
(2)求过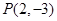 点且与直线
点且与直线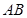 平行的直线
平行的直线 的方程;
的方程;
(3)一束光线从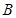 点射向(Ⅱ)中的直线
点射向(Ⅱ)中的直线 ,若反射光线过点
,若反射光线过点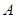 ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
(本小题14分)已知f(x)=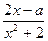 (x∈R)在区间[-1,1]上是增函数,
(x∈R)在区间[-1,1]上是增函数,
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
的两个非零实根为x1、x2。试问:是否存在实数m,使得不等
式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
(本小题13分)已知函数 与
与 的图象相交于
的图象相交于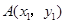 ,
,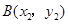 ,
, ,
,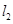 分别是
分别是 的图象在
的图象在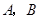 两点的切线,
两点的切线, 分别是
分别是 ,
,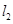 与
与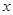 轴的交点.
轴的交点.
(1)求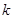 的取值范围;
的取值范围;
(2)设 为点
为点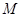 的横坐标,当
的横坐标,当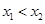 时,写出
时,写出 以
以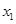 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(3)试比较 与
与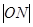 的大小,并说明理由(
的大小,并说明理由(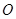 是坐标原点).
是坐标原点).
(本小题12分)已知二次函数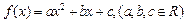 满足:对任意实数x,都有
满足:对任意实数x,都有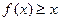 ,且当
,且当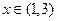 时,有
时,有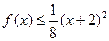 成立.
成立.
(1)求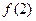 ;
;
(2)若 的表达式;
的表达式;
(3)设 ,若
,若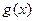 图上的点都位于直线
图上的点都位于直线 的上方,求实
的上方,求实
数m的取值范围。
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t(件),价格近似满足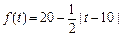 (元).
(元).
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
(本小题12分)设不等式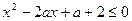 的解集为M,如果M
的解集为M,如果M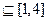 ,求实数
,求实数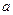 的取值范围.
的取值范围.