已知中心在原点,焦点在坐标轴上的双曲线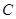 经过
经过 、
、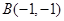 两点
两点
(1)求双曲线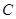 的方程;
的方程;
(2)设直线 交双曲线
交双曲线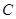 于
于 、
、 两点,且线段
两点,且线段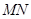 被圆
被圆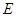 :
: 三等分,求实数
三等分,求实数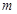 、
、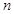 的值
的值
(本小题满分12分)如图,已知四棱锥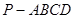 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,
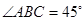 ,
, ,
, ,
,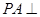 平面
平面 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)若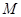 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.
(本小题满分12分)某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(Ⅰ)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(Ⅱ)设甲篮球运动员10场比赛得分平均值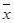 ,将10场比赛得分
,将10场比赛得分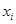 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的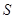 大小为多少?并说明
大小为多少?并说明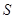 的统计学意义;
的统计学意义;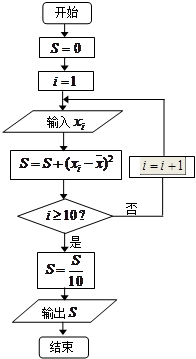
(Ⅲ)如果从甲、乙两位运动员的10场得分中,各随机抽取一场不小于30分的得分,求甲的得分大于乙的得分的概率.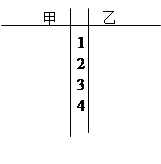
本小题满分12分)设直线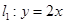 与直线
与直线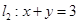 交于P点.
交于P点.
(Ⅰ)当直线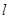 过P点,且与直线
过P点,且与直线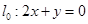 平行时,求直线
平行时,求直线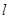 的方程.
的方程.
(Ⅱ)当直线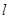 过P点,且原点O到直线
过P点,且原点O到直线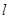 的距离为1时,求直线
的距离为1时,求直线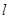 的方程.
的方程.
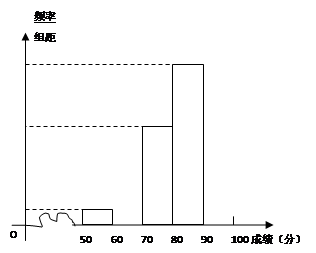
本小题满分12分)青少年“心理健康”问题越来越引起社会关注,某校对高二600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(Ⅰ)填写答题卡频率分布表中的空格,并补全频率分布直方图;
(Ⅱ)试估计该年段成绩在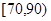 段的有多少人?
段的有多少人?
(Ⅲ)请你估算该年段分数的众数.
| 分 组 |
频 数 |
频 率 |
| [50,60) |
2 |
0.04 |
| [60,70) |
8 |
0.16 |
| [70,80) |
10 |
|
| [80,90) |
||
| [90,100] |
14 |
0.28 |
| 合 计 |
1.00 |
已知函数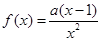 ,其中
,其中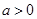 .
.
(1)求函数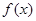 的单调区间;
的单调区间;
(2)若直线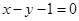 是曲线
是曲线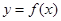 的切线,求实数
的切线,求实数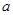 的值;
的值;
(3)设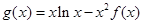 ,求
,求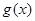 在区间
在区间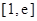 上的最小值.(其中
上的最小值.(其中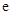 为自然对数的底数)
为自然对数的底数)