如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2.四边形ABCD满足BC∥AD,AB⊥AD,AB=BC=1.点E,F分别为侧棱PB,PC上的点,且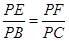 =λ.
=λ.
(1)求证:EF∥平面PAD.
(2)当λ= 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;
(3)是否存在实数λ,使得平面AFD⊥平面PCD?若存在,试求出λ的值;若不存在,请说明理由.
(本小题满分12分)
如图,在等边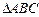
 中,O为边
中,O为边 的中点,
的中点, ,D、E为
,D、E为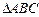 的高线上的点,且
的高线上的点,且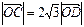 ,
, .若以A,B为焦点,O为中心的椭圆过点D,建立适当的直角坐标系,记椭圆为M
.若以A,B为焦点,O为中心的椭圆过点D,建立适当的直角坐标系,记椭圆为M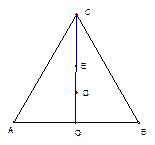
(1)求椭圆M的方程;
(2)过点E的直线 与椭圆M交于不同的两点P,Q,点P在点E, Q之
与椭圆M交于不同的两点P,Q,点P在点E, Q之
间,且 ,求实数
,求实数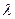 的取值范围.
的取值范围.
(本小题满分12分)
已知数列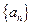 是各项不为0的等差数列,
是各项不为0的等差数列,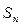 为其前n
为其前n
项和,且满足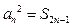 , 令
, 令 ,数列
,数列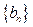 的
的
前n项和为
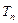 .
.
(1)求数列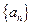 的通项公式及数列
的通项公式及数列 的前n项和
的前n项和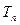 ;
;
(2) 是否存在正整数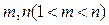 ,使得
,使得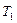 ,
, ,
,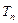 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的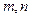 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
如图,四棱柱 中,
中, 平面
平面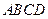 ,底面
,底面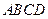 是边长为
是边长为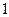 的正方形,侧棱
的正方形,侧棱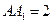 .
.
(1)求证: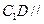 平面
平面 ;
;
(2)求直线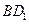 与平面
与平面 所成角的正弦值.
所成角的正弦值.
.(本小题满分12分)
在“自选模块”考试中,某考场的每位同学都选作了一道数学题,第一小组选《不等式选讲》的有1人,选《坐标系与参数方程 》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4 人均为选《坐标系与参数方程》的概率;
(2)设 为选出的4个人中选《不等式选讲》的人数,求
为选出的4个人中选《不等式选讲》的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)
已知向量 设
设 (
( ,且
,且 为常数).
为常数).
(1)求 的最小正周期;
的最小正周期;
(2)若 在
在 上的最大值与最小值之和为7,求
上的最大值与最小值之和为7,求 的值.
的值.