已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若方程 有解,求实数m的取值范围;
有解,求实数m的取值范围;
(3)若存在实数 ,使
,使 成立,求证:
成立,求证: .
.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,说明它表示什么曲线。
(Ⅰ)已知函数 ,若存在
,若存在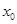 ,使得
,使得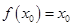 ,则称
,则称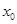 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数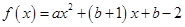 .
.
(Ⅰ) 当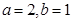 时,求函数
时,求函数 的不动点;
的不动点;
(Ⅱ) 若对于任意实数 ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数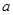 的取值范围;
的取值范围;
(Ⅲ) 在(Ⅱ)的条件下,若函数 的图象上
的图象上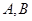 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线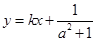 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数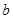 的取值范围.
的取值范围.
定义在R上的单调函数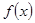 满足
满足 且对任意
且对任意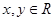 都有
都有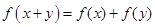 .
.
(1)求证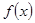 为奇函数;
为奇函数;
(2)若 对任意
对任意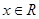 恒成立,求实数
恒成立,求实数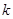 的取值范围.
的取值范围.
设函数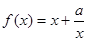 定义域为
定义域为 ,且
,且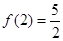 .设点
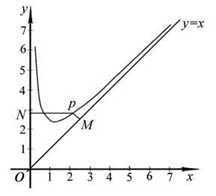
.设点 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 分别作直线
分别作直线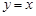 和
和 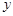 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.
(1)写出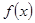 的单调递减区间(不必证明);
的单调递减区间(不必证明);
(2)问: 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设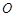 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.
面积的最小值.
设函数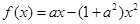 ,其中
,其中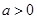 ,区间
,区间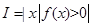
(Ⅰ)求的长度(注:区间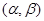 的长度定义为
的长度定义为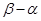 );
);
(Ⅱ)给定常数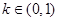 ,当时,求长度的最小值.
,当时,求长度的最小值.