如图,小丽在观察某建筑物 .
.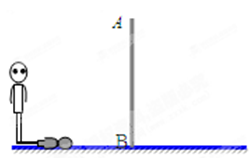
(1)请你根据小亮在阳光下的投影,画出建筑物 在阳光下的投影.
在阳光下的投影.
(2)已知小丽的身高为 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物 的投影长分别为
的投影长分别为 和
和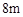 ,求建筑物
,求建筑物 的高.
的高.
已知,如图:△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD、BD,过D作DH⊥AB,垂足为H,交AC于E.
(1)若△ABD是等边三角形,求DE的长;
(2)若BD=AB,且tan∠HDB=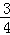 ,求DE的长.
,求DE的长.
如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: ≈1.732)
≈1.732)
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,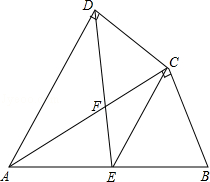
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求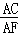 的值.
的值.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F, .
.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
如图,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.
(1)求AB的长;
(2)求CD的长;
(3)求∠BAD的大小.