对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
(本小题满分12分)已知函数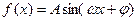
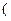
 ,
, ,
,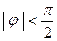
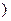
在一个周期内,当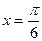 时,
时,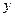 有最大值为
有最大值为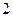 ,当
,当 时,
时,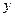 有最小值为
有最小值为  .
.
(1)求函数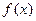 表达式;
表达式;
(2)若 ,求
,求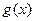 的单调递减区间.
的单调递减区间.
(本小题满分12分)甲乙两人各有 个材质、大小、形状完全相同的小球,甲的
个材质、大小、形状完全相同的小球,甲的
小球上面标有 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有 五个数字.把各自的小球放
五个数字.把各自的小球放
入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小
个小球.规定:若甲摸出的小
球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间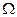 ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
(本小题满分12分)已知点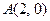 ,
,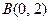 ,点
,点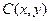 在单位圆上.
在单位圆上.
(1)若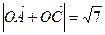 (
(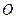 为坐标原点),求
为坐标原点),求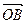 与
与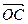 的夹角;
的夹角;
(2)若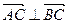 ,求点
,求点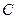 的坐标.
的坐标.
(本小题满分12分)为了调查甲、乙两种品牌商品的市场认可度,在某购物网点
随机选取了14天,统计在某确定时间段的销量,得如下所示的统计图,根据统计图求:
(1)甲、乙两种品牌商品销量的中位数分别是多少?
(2)甲品牌商品销量在[20,50]间的频率是多少?
(3)甲、乙两个品牌商品哪个更受欢迎?并说明理由.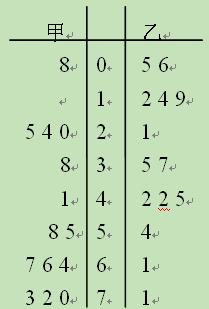
(本小题满分12分)已知圆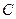 与直线
与直线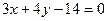 相切于点
相切于点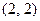 ,其圆心
,其圆心
在直线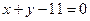 上,求圆
上,求圆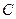 的方程.
的方程.