如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.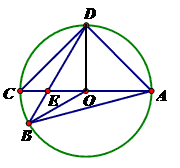
(1)求∠BOD的度数及点O到BD的距离;
(2)若DE=2BE,求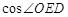 的值.
的值.
计算:
某班组织20位同学去帮助某果园的果农采摘柑橘,任务是完成720千克柑橘的采摘、运送、包装三项工作,根据实际情况将三项工作的人员分配制成统计图,每人每小时完成某项工作量制作如下统计图: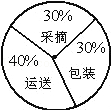
(1)按照如图的人员分配方案,已知各项工作完成的时间相等,那么问每人每小时运送、包装各多少千克柑橘并补全条形统计图;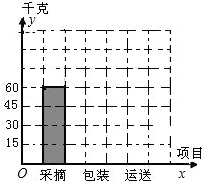
(2)若他们一起完成采摘任务后,小明同学将20人分成两组,一组运送,一组去包装,结果当负责运送的一组完成了任务时,另一个组在相等的时间内还有80千克的柑橘还没有包装,试问小明是怎样将人员分配的?
如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,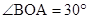
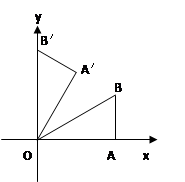
(1)求点B和点A′的坐标;
(2)求经过点B和点B′的直线所对应的一次函数解析式,并判断点A是否在直线BB′上。
如图,抛物线C1:y=ax2+bx+1的顶点坐标为D(1,0),
(1)求抛物线C1的解析式;
(2)如图1,将抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,直线y=x+c,经过点D交y轴于点A,交抛物线C2于点B,抛物线C2的顶点为P,求△DBP的面积;
(3)如图2,连接AP,过点B作BC⊥AP于C,设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC·(AC+EC)为定值.
如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).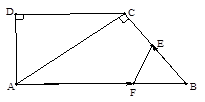
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.