如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1= .
.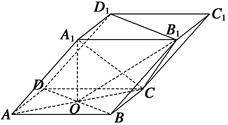
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
对于数列 若存在常数M>0,对任意的 ,恒有 则称数列 为B-数列
(1)首项为1,公比为 的等比数列是否为B-数列?请说明理由;
请以其中一组的一个论断条件,另一组中的一个论断为结论组成一个命题
判断所给命题的真假,并证明你的结论;
(2)设 是数列 的前 项和,给出下列两组论断;
A组:①数列 是B-数列 ②数列 不是B-数列
B组:③数列 是B-数列 ④数列 不是B-数列
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题。
判断所给命题的真假,并证明你的结论;
(3)若数列 都是 数列,证明:数列 也是 数列。
在平面直角坐标系 中,点P到点F 的距离的4倍与它到直线 的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标与18之和
(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线I与轨迹C相交于M,N两点,求线段MN长度的最大值。
某地建一座桥,两端的桥墩已建好,这两墩相距 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,距离为 米的相邻两墩之间的桥面工程费用为 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为 万元。
(Ⅰ)试写出 关于 的函数关系式;
(Ⅱ)当 =640米时,需新建多少个桥墩才能使 最小?
如下图,在正三棱柱 中, ,D是 的中点,点E在 上,且 。

(1)证明:平面 平面
(2)求直线 和平面 所成角的正弦值。
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的 、 、 ,现在3名工人独立地从中任选一个项目参与建设。
(1)求他们选择的项目所属类别互不相同的概率;
(2)记 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求 的分布列及数学期望。