假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p0.
(1)求p0的值;(参考数据:若X~N(μ,σ2),有P(μ-σ<X≤μ+σ)=0.682 6,P(μ-2σ<X≤μ+2σ)=0.954 4,P(μ-3σ<X≤μ+3σ)=0.997 4)
(2)某客运公司用A、B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次.A、B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆?
如图,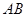 为圆
为圆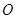 的直径,点
的直径,点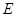 、
、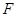 在圆
在圆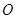 上,矩形
上,矩形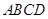 所在的平面和圆
所在的平面和圆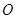 所在的平面互相垂直,且
所在的平面互相垂直,且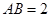 ,
, .
.
(Ⅰ)求证: 平面
平面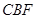 ;
;
(Ⅱ)求三棱锥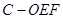 的体积.
的体积.
某地三所高中校A、B、C联合组织一项活动,用分层抽样方法从三所学校的相关人员中,抽取若干人组成领导小组,有关数据如下表(单位:人)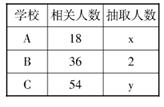
(Ⅰ)求x,y;
(Ⅱ)若从B、C两校抽取的人中选 人任领导小组组长,求这二人都来自学校C的概率.
人任领导小组组长,求这二人都来自学校C的概率.
已知函数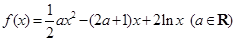 .
.
(Ⅰ)若曲线 在
在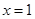 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在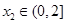 ,使得
,使得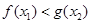 ,求
,求 的取值范围.
的取值范围.
如图,F1,F2是离心率为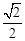 的椭圆C:
的椭圆C: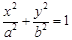 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线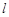 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1 :3.设A,B是椭圆C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 :3.设A,B是椭圆C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.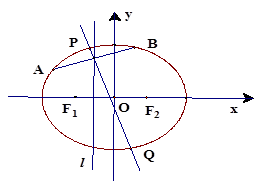
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 求 的取值范围.
的取值范围.
某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
| 付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
 |
10 |
 |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润。
(Ⅰ)求上表中 的值;
的值;
(Ⅱ)若以频率作为概率,求事件 :“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率 ;
;
(Ⅲ)求Y的分布列及数学期望EY.