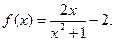设椭圆
的右焦点为
，直线
与
轴交于点
，若
（其中
为坐标原点）．
（1）求椭圆
的方程；
（2）设
是椭圆上的任意一点，
为圆
的任意一条直径（
、
为直径的两个端点），求
的最大值．
有甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40km的B处，乙厂到河岸的垂足D与A相距50km，两厂要在此岸边合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，问供水站C建在岸边何处才能使水管费用最省？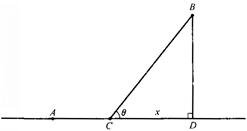
已知函数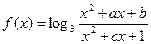
，是否存在实数a、b、c，使
同时满足下列三个条件：（1）定义域为R的奇函数；（2）在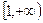
上是增函数；（3）最大值是1．若存在，求出a、b、c；若不存在，说明理由．
已知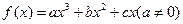
在
时取得极值，且
．
（1）试求常数a、b、c的值；
（2）试判断是函数的极小值还是极大值，并说明理由．
求下列函数的极值：
（1）
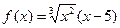；（2）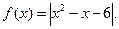
求下列函数的极值：
（1）
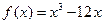；（2）
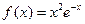；（3）