如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,且AE=MC=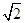 .
.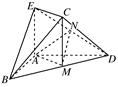
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
如右图所示,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=.
(1)求证:PA⊥平面ABCD;
(2)求四棱锥P-ABCD的体积
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.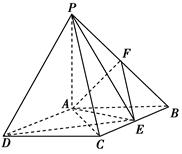
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
如右图所示,ABCD-A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点.
(1)求证:BD1∥平面C1DE;
(2)求三棱锥D-D1BC的体积.
(本大题共14分)
已知函数 (
( 为实常数)的两个极
为实常数)的两个极 值点为
值点为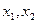 ,且满足
,且满足
(1)求 的取值范围;
的取值范围;
(2)比较 与
与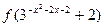 的大小.
的大小.
本大题共13分)
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两 个岗位没有被选的概率;
个岗位没有被选的概率;
(2)设选择A岗位的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。