已知中心在原点的双曲线C的一个焦点是F1(一3,0),一条渐近线的方程是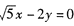
(1)求双曲线C的方程;
(2)若以k(k≠0)为斜率的直线 与双曲线C相交于两个不同的点M, N,且线段MN的
与双曲线C相交于两个不同的点M, N,且线段MN的
垂直平分线与两坐标轴围成的三角形的面积为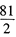 ,求k的取值范围。
,求k的取值范围。
(本小题满分14分)如图,在四棱锥P - ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:
(1)PA∥平面MDB;
(2)PD⊥BC.
(本小题满分14分)某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
(本小题满分14分)已知圆的圆心为坐标原点,且经过点(-1, ).
).
(1)求圆的方程;
(2)若直线 与此圆有且只有一个公共点,求
与此圆有且只有一个公共点,求 的值;
的值;
(3)求直线 被此圆截得的弦长.
被此圆截得的弦长.
设数列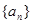 的前
的前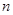 项的和
项的和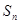 ,已知
,已知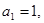
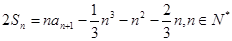 .
.
(1)求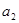 的值;
的值;
(2)证明:数列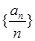 是等差数列,并求出数列
是等差数列,并求出数列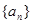 的通项公式;
的通项公式;
(3)证明:对一切正整数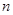 ,有
,有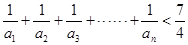 .
.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{xn}.
(1)若定义函数 ,且输入
,且输入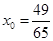 ,请写出数列{xn}的所有项;
,请写出数列{xn}的所有项;
(2)若定义函数f(x)=xsinx(0≤x≤2π),且要产生一个无穷的常数列{xn},试求输入的初始数据x0的值及相应数列{xn}的通项公式xn;
(3)若定义函数f(x)=2x+3,且输入x0=﹣1,求数列{xn}的通项公式xn.