如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是矩形,SD=AD=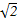 AB,E是SA的中点.
AB,E是SA的中点.
(1)求证:平面BED⊥平面SAB.
(2)求直线SA与平面BED所成角的大小.
在平面直角坐标系 中,原点为
中,原点为 ,抛物线
,抛物线 的方程为
的方程为 ,线段
,线段 是抛物线
是抛物线 的一条动弦.
的一条动弦.
(1)求抛物线 的准线方程和焦点坐标
的准线方程和焦点坐标 ;
;
(2)若 ,求证:直线
,求证:直线 恒过定点;
恒过定点;
(3)当 时,设圆
时,设圆 ,若存在且仅存在两条动弦
,若存在且仅存在两条动弦 ,满足直线
,满足直线 与圆
与圆 相切,求半径
相切,求半径 的取值范围?
的取值范围?
定义函数 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数 的短距.
的短距.
(1)分别判断函数 与
与 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;
(2)求证:指数函数 的短距小于1;
的短距小于1;
(3)对于任意 是否存在实数
是否存在实数 ,使得函数
,使得函数 的短距不小于2,若存在,请求出
的短距不小于2,若存在,请求出 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?
数列 的首项
的首项 ,
,
求数列 的通项公式;
的通项公式;
设 的前
的前 项和为
项和为 ,求
,求 的最小值.
的最小值.
如图,某污水处理厂要在一正方形污水处理池 内修建一个三角形隔离区以投放净化物质,其形状为三角形
内修建一个三角形隔离区以投放净化物质,其形状为三角形 ,其中
,其中 位于边
位于边 上,
上, 位于边
位于边 上.已知
上.已知 米,
米, ,设
,设 ,记
,记 ,当
,当 越大,则污水净化效果越好.
越大,则污水净化效果越好.
(1)求 关于的函数解析式,并求定义域;
关于的函数解析式,并求定义域;
(2)求 最大值,并指出等号成立条件?
最大值,并指出等号成立条件?
直三棱柱 的底面为等腰直角三角形,
的底面为等腰直角三角形, ,
, ,
, 分别是
分别是 的中点。求异面直线
的中点。求异面直线 和
和 所成角的大小。
所成角的大小。