为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0~1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
| 鱼的 质量 |
[1.00, 1.05) |
[1.05, 1.10) |
[1.10, 1.15) |
[1.15, 1.20) |
[1.20, 1.25) |
[1.25, 1.30) |
| 鱼的 条数 |
3 |
20 |
35 |
31 |
9 |
2 |
(1)根据数据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否存在问题?
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
计算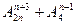 的值.
的值.
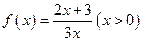


⑴求数列 的通项公式;
的通项公式;
⑵设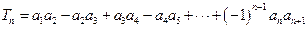 ,若
,若 对
对 恒成立,求实数
恒成立,求实数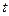 的取值范围;
的取值范围;
⑶是否存在以 为首项,公比为
为首项,公比为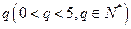 的数列
的数列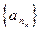 ,
,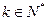 ,使得数列
,使得数列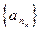 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由



⑴求函数 的解析式;
的解析式;
⑵若对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数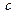 的最小值;
的最小值;
⑶若过点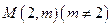 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围
的取值范围

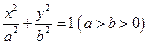




⑴求椭圆 的方程;
的方程;
⑵设 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心,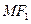 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线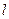 有公共点时,求△
有公共点时,求△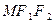 面积的最大值
面积的最大值
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AB=BC= ,BB1=3,D为A1C1的中点,F在线段AA1上.
,BB1=3,D为A1C1的中点,F在线段AA1上.
(1)AF为何值时,CF⊥平面B1DF?
(2)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值.