在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.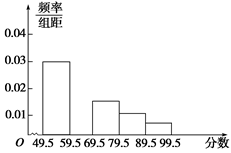
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数是多少;
(3)这两个班参赛学生的成绩的中位数应落在第几小组内.
己知在锐角ΔABC中,角 所对的边分别为
所对的边分别为 ,且
,且
(I )求角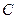 大小;
大小;
(II)当 时,求
时,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-5:不等式选讲
设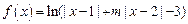 (
( ).
).
(Ⅰ)当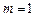 时,求函数
时,求函数 的定义域;
的定义域;
(Ⅱ)若当 ,
,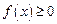 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
如图,已知点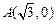 ,
, ,圆
,圆 是以
是以 为直径的圆,直线
为直径的圆,直线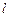 :
: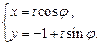
( 为参数).
为参数).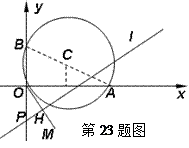
(Ⅰ)写出圆 的普通方程并选取适当的参数改写为参数方程;
的普通方程并选取适当的参数改写为参数方程;
(Ⅱ)过原点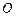 作直线
作直线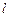 的垂线,垂足为
的垂线,垂足为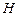 ,若动点
,若动点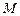 满足
满足 ,当
,当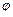 变化时,求点
变化时,求点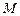 轨迹的参数方程,并指出它是什么曲线.
轨迹的参数方程,并指出它是什么曲线.
(本小题满分10分)选修4-1:几何证明选讲
如图,已知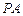 与圆
与圆 相切于点
相切于点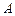 ,半径
,半径 ,
, 交
交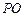 于点
于点 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若圆 的半径为3,
的半径为3, ,求
,求 的长度.
的长度.
(本小题满分12分)
已知函数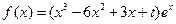 ,
,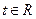 .依次在
.依次在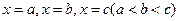 处取到极值.
处取到极值.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)若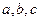 成等差数列,求
成等差数列,求 的值.
的值.