设椭圆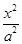 +
+ =1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
(1)求椭圆的离心率e;
(2)设直线PF2与椭圆相交于A,B两点.若直线PF2与圆(x+1)2+(y- )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ ,
, ,平面
,平面 ⊥底面
⊥底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点, ,
, ,
, .
.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)若 为棱
为棱 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
某企业招聘工作人员,设置 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加 组测试,丙、丁两人各自独立参加
组测试,丙、丁两人各自独立参加 组测试.已知甲、乙两人各自通过测试的概率均为
组测试.已知甲、乙两人各自通过测试的概率均为 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加 组测试,
组测试, 组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
组共有6道试题,戊会其中4题.戊只能且必须选择4题作答,答对3题则竞聘成功.
(Ⅰ)求戊竞聘成功的概率;
(Ⅱ)求参加 组测试通过的人数多于参加
组测试通过的人数多于参加 组测试通过的人数的概率;
组测试通过的人数的概率;
(Ⅲ)记 、
、 组测试通过的总人数为
组测试通过的总人数为 ,求
,求 的分布列和期望.
的分布列和期望.
已知平面向量 ,
, ,
, ,其中
,其中 ,且函数
,且函数 的图象过点
的图象过点 .
.
(1)求 的值;
的值;
(2)将函数 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
四棱锥 中,
中, ⊥底面
⊥底面 ,
, ,
, ,
, .
.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)若侧棱 上的点
上的点 满足
满足 ,求三棱锥
,求三棱锥 的体积.
的体积.
一个多面体的直观图、正视图、侧视图、俯视图如图所示,M、N分别为A1B、B1C1的中点.
(1)求证:MN//平面ACC1A1;
(2)求证:MN^平面A1BC.