如图已知抛物线 :
: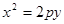 过点
过点 ,直线
,直线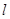 交
交 于
于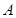 ,
,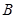 两点,过点
两点,过点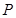 且平行于
且平行于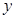 轴的直线分别与直线
轴的直线分别与直线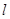 和
和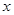 轴相交于点
轴相交于点 ,
, .
.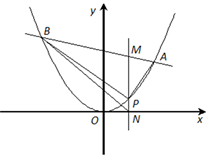
(1)求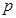 的值;
的值;
(2)是否存在定点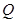 ,当直线
,当直线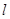 过点
过点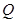 时,△
时,△ 与△
与△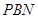 的面积相等?若存在,求出点
的面积相等?若存在,求出点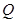 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知函数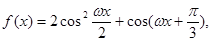 (其中
(其中 的最小正周期为
的最小正周期为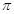 .
.
(Ⅰ)求 的值,并求函数
的值,并求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)在锐角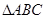 中,
中,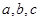 分别是角
分别是角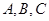 的对边,若
的对边,若
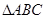 的面积为
的面积为 ,求
,求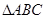 的外接圆面积.
的外接圆面积.
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率直方图(如图),其中,上学所需时间的范围是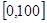 ,样本数据分组为
,样本数据分组为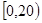 ,
, ,
, ,
,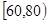 ,
,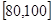 .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不小于1小时的学生中可以申请在学校住宿,请估计学校
名新生中有多少名学生可以住宿.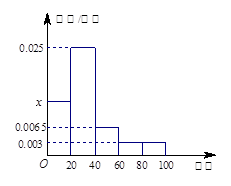
(本小题满分10分)选修4-5:不等式选讲
对于任意的实数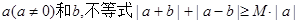 恒成立,记实数M的
恒成立,记实数M的
最大值是m.
(1)求m的值;
(2)解不等式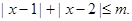
(本小题满分10分)选修4-4:坐标系与参数方程
已知直线 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.
(I)求圆心C的直角坐标;
(Ⅱ)由直线 上的点向圆C引切线,求切线长的最小值.
上的点向圆C引切线,求切线长的最小值.
(本小题满分10分)选修4-1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE=EF.