已知直线l1:x-2y-1=0,直线l2:ax-by+1=0,其中a,b∈{1,2,3,4,5,6}.
(1) 求直线l1与l2相交的概率;
(2) 求直线l1与l2的交点位于第一象限的概率.
已知ΔABC的三个内角A,B,C所对的边长分别为a,b,c.且A,C,B依次成等差数列,c=2。
(1).若ΔABC的面积等于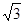 ,求边长a , b ;(2).若
,求边长a , b ;(2).若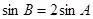 ,求ΔABC的面积.
,求ΔABC的面积.
已知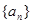 是等差数列,其中
是等差数列,其中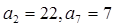 (1).求
(1).求 的通项;
的通项;
(2).求 值;(3)设数列
值;(3)设数列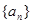 的前
的前 项和为
项和为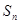 ,求
,求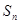 的最大值。
的最大值。

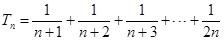
(1)求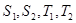 ;
;
(2)猜想 与
与 的关系,并用数学归纳法证明。
的关系,并用数学归纳法证明。
对某校小学生进行心理障碍测试得到如下的列联表:
| 有心理障碍 |
没有心理障碍 |
总计 |
|
| 女生 |
10 |
30 |
|
| 男生 |
70 |
80 |
|
| 总计 |
20 |
110 |
将表格填写完整,试说明心理障碍与性别的关系?
附:
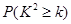 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3. 841 |
5.024 |
6.635 |
7.879 |
10.828 |
解关于 的不等式:
的不等式: