已知数列{an}是等差数列,数列{bn}是等比数列,且对任意的 ,都有
,都有
 .
.
(1)若{bn }的首项为4,公比为2,求数列{an+bn}的前n项和Sn;
(2)若 ,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它
,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由.
(本小题满分15分) 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=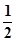 AD=1,CD=
AD=1,CD=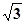 .
.
(Ⅰ)求证:平面PQB⊥平面P AD;
AD;
(Ⅱ)设PM="t" MC,若二面角M-BQ-C的平面角的大小为30°,试确定t的值.
(本小题满分14分)已知数列 是递增数列,且满足
是递增数列,且满足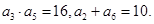
(Ⅰ)若 是等差数列,求数列
是等差数列,求数列 的通
的通 项公式;
项公式;
(Ⅱ)对于(Ⅰ)中 ,令
,令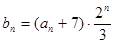 ,求数列
,求数列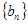 的前
的前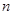 项和
项和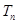 .
.
(本小题满分14分)在钝角三角形ABC中,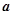 、
、 、
、 分别是角A、B、C的对边,
分别是角A、B、C的对边,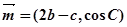 ,
,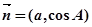 ,且
,且 ∥
∥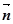 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求函数 的值域.
的值域.
已知双曲线方程为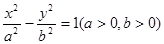 ,椭圆C以该双曲线的焦点为顶点,顶点为焦点。
,椭圆C以该双曲线的焦点为顶点,顶点为焦点。
(1)当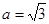 ,
, 时,求椭圆C的方程;
时,求椭圆C的方程;
(2)在(1)的条件下,直线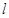 :
: 与
与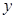 轴交于点P,与椭圆交与A,B两点,若O为坐标原点,
轴交于点P,与椭圆交与A,B两点,若O为坐标原点,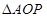 与
与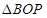 面积之比为2:1,求直线
面积之比为2:1,求直线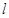 的方程;
的方程;
(3)若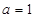 ,椭圆C与直线
,椭圆C与直线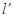 :
: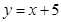 有公共点,求该椭圆的长轴长的最小值。
有公共点,求该椭圆的长轴长的最小值。
动圆C的方程为 。
。
(1)若 ,且直线
,且直线 与圆C交于A,B两点,求弦长
与圆C交于A,B两点,求弦长 ;
;
(2)求动圆圆心C的轨迹方程;
(3)若直线 与动圆圆心C的轨迹有公共点,求
与动圆圆心C的轨迹有公共点,求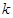 的取值范围。
的取值范围。