如图,正三棱柱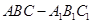 的底面边长是
的底面边长是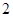 ,侧棱长是
,侧棱长是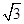 ,
,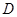 是
是 的中点.
的中点.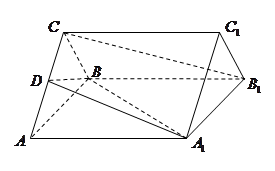
(1)求证: ∥平面
∥平面 ;
;
(2)求二面角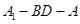 的大小;
的大小;
(3)在线段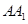 上是否存在一点
上是否存在一点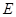 ,使得平面
,使得平面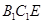
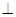 平面
平面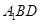 ,若存在,求出
,若存在,求出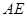 的长;若不存在,说明理由.
的长;若不存在,说明理由.
已知抛物线C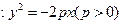 上横坐标为
上横坐标为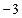 的一点,与其焦点的距离为4.(1)求
的一点,与其焦点的距离为4.(1)求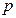 的值;(2)设动直线
的值;(2)设动直线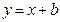 与抛物线C相交于A.B两点,问在直线
与抛物线C相交于A.B两点,问在直线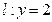 上是否存在与
上是否存在与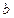 的取值无关的定点M,使得
的取值无关的定点M,使得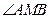 被直线
被直线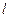 平分?若存在,求出点M的坐标;若不存在,说明理由.
平分?若存在,求出点M的坐标;若不存在,说明理由.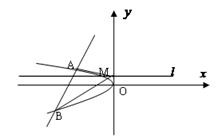
如图,在矩形ABCD中,AB=2,AD=1,E为CD的中点,将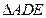 沿AE折起,使平面
沿AE折起,使平面 平面ABCE,得到几何体
平面ABCE,得到几何体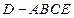 .(1)求证:
.(1)求证: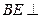 平面
平面 ;(2)求BD和平面
;(2)求BD和平面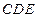 所成的角的正弦值.
所成的角的正弦值.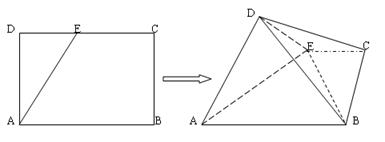
甲从装有编号为1,2,3,4,5的卡片的箱子中任意取一张,乙从装有编号为2,4的卡片的箱子中任意取一张,用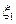 ,
,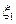 分别表示甲.乙取得的卡片上的数字.(1)求概率
分别表示甲.乙取得的卡片上的数字.(1)求概率
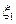
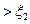 );(2)记
);(2)记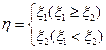 ,求
,求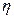 的分布列与数学期望.
的分布列与数学期望.
设函数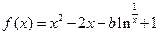 其中b为常数
其中b为常数
(1)当 时,判断函数
时,判断函数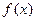 在定义域上的单调性
在定义域上的单调性
(2)若函数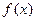 有极值点,求b的取值范围,以及
有极值点,求b的取值范围,以及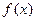 的极值点
的极值点
设函数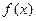 的定义域、值域均为
的定义域、值域均为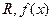 的反函数为
的反函数为 ,且对任意的
,且对任意的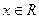 ,均有
,均有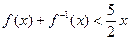 ,定义数列
,定义数列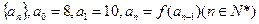
(1)求证: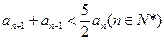
(2)设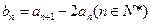 求证
求证
(3)是否存在常数A、B同时满足: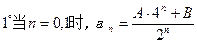 ,
,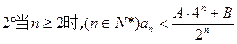 如果存在,求出A、B的值,如果不存在,说明理由。
如果存在,求出A、B的值,如果不存在,说明理由。