(本小题满分12分)
直四棱柱 中,底面
中,底面 为菱形,且
为菱形,且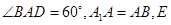 为
为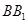 延长线上的一点,且
延长线上的一点,且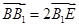 .
.
(Ⅰ)求证: 面
面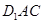 ;
;
(Ⅱ)在棱 是否存在一点
是否存在一点 ,使
,使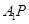
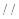 面
面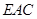 ?若存在,求
?若存在,求 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(Ⅲ)求二面角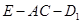 的大小;
的大小;
已知 ,
, 的图象向右平移
的图象向右平移 个单位再向下平移
个单位再向下平移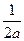 个单位后得到函数
个单位后得到函数 的图象。
的图象。
(Ⅰ)求函数 的表达式;(Ⅱ)当
的表达式;(Ⅱ)当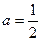 时,求
时,求 在区间
在区间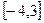 上的最大值与最小值;
上的最大值与最小值;
( Ⅲ)若函数 上的最小值为
上的最小值为 的最大值。
的最大值。
已知函数 。(1)判断函数
。(1)判断函数 的奇偶性;
的奇偶性;
(2)设
 ,求证:对于任意
,求证:对于任意 ,都有
,都有 。
。
求


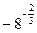 的值
的值
已知椭圆 的离心率
的离心率 ,过A(a,0),
,过A(a,0),
B(0,-b),两点的直线到原点的距离是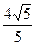 .
.
⑴求椭圆的方程 ;
⑵已知直线y=kx+1(k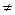 0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.
0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.
已知 、
、 为椭圆
为椭圆 的左右顶点,
的左右顶点, 为椭圆的右焦点,
为椭圆的右焦点, 是椭圆上异于
是椭圆上异于 、
、 的任意一点,直线
的任意一点,直线 、
、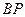 分别交直线
分别交直线 于
于 、
、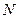 两点,
两点, 交
交 轴于
轴于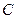 点.
点.
(Ⅰ)当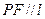 时,求直线
时,求直线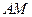 的方程;
的方程;
(Ⅱ)是否存在实数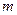 ,使得以
,使得以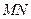 为直径的圆过点
为直径的圆过点 ,若存在,求出实数
,若存在,求出实数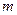 的值;,若不存在,请说明理由;
的值;,若不存在,请说明理由;