（本小题满分12分）【改编自广东省广州市海珠区2014届高三-优题课

题文

（本小题满分12分）
【改编自广东省广州市海珠区2014届高三入学摸底考试数学试题第17题】为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各9件样品，测量产品中某种元素的含量（单位：毫克），如图是测量数据的茎叶图，但是乙厂记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以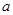表示，规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品.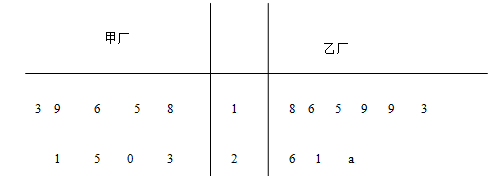

（Ⅰ）若甲、乙两厂产品中该种元素含量的平均值相同，求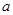的值；
（Ⅱ）求乙厂该种元素含量的平均值超过甲厂平均值的概率；
（Ⅲ）当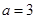时，利用简单随机抽样的方法,分别在甲、乙两厂该种元素含量超过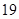（毫克）的数据中个抽取一个做代表,设抽取的两个数据中超过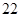（毫克）的个数最多不超过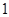个的概率.

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

如图，在五面体 $A B C D E F$ 中， $A B / / D C$ ， $∠ B A D = \frac{π}{2}$ ， $C D = A D = 2$ ，四边形 $A B F E$ 为平行四边形， $F A ⊥$ 平面 $A B C D$ ， $F C = 3, E D = \sqrt{7}$ ．求：

（Ⅰ）直线 $A B$ 到平面 $E F C D$ 的距离；
（Ⅱ）二面角 $F - A D - E$ 的平面角的正切值．

袋中有大小、形状相同的红、黑球各一个，现一次有放回地随机摸取3次，每次摸取一个球
（I）试问：一共有多少种不同的结果？请列出所有可能的结果；
（Ⅱ）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率。

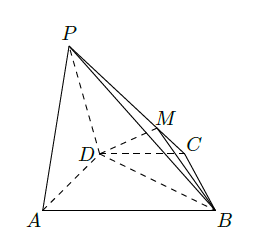
如图,在四棱锥 $P - A B C D$ 中,平面 $P A D ⊥$ 平面 $A B C D$ , $A B ∥ D C$ , $∆ P A D$ 是等边三角形,已知 $B D = 2 A D = 8, A B = 2 D C = 4 \sqrt{5}$ ．

（Ⅰ）设 $M$ 是 $P C$ 上的一点,证明:平面 $M B D ⊥$ 平面 $P A D$ ；
（Ⅱ）求四棱锥 $P - A B C D$ 的体积．

设函数 $f (x) = (\sin ω x + \cos ω x)^{2} + 2 \cos^{2} ω x (ω > 0)$ 的最小正周期为 $\frac{2 π}{3}$ ．
（Ⅰ）求 $ω$ 的最小正周期．
（Ⅱ）若函数 $y = g (x)$ 的图像是由 $y = f (x)$ 的图像向右平移 $\frac{π}{2}$ 个单位长度得到，求 $y = g (x)$ 的单调增区间．

等比数列 ${a_{n}}$ 中，已知 $a_{1} = 2, a_{4} = 16$ .
（I）求数列 ${a_{n}}$ 的通项公式；
（Ⅱ）若 $a_{3}, a_{5}$ 分别为等差数列 ${b_{n}}$ 的第3项和第5项，试求数列 ${b_{n}}$ 的通项公式及前 $n$ 项和 $S_{n}$ .

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号