某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有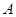 、
、 两个定点投篮位置,在
两个定点投篮位置,在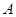 点投中一球得2分,在
点投中一球得2分,在 点投中一球得3分.其规则是:按先
点投中一球得3分.其规则是:按先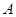 后
后 再
再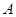 的顺序投
的顺序投
篮.教师甲在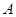 和
和 点投中的概率分别是
点投中的概率分别是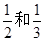 ,且在
,且在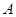 、
、 两点投中与否相互独立.
两点投中与否相互独立.
(1)若教师甲投篮三次,试求他投篮得分X的分布列和数学期望;
(2)若教师乙与甲在A、B点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
已知函数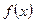 是定义在
是定义在 上的奇函数,并且在
上的奇函数,并且在 上是减函数.是否存在实数
上是减函数.是否存在实数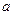 使
使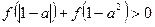 恒成
恒成 立?若存在,求出实数
立?若存在,求出实数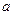 的取值范围;若不存在,请说明理由.[来
的取值范围;若不存在,请说明理由.[来
我国是水资源比较贫乏的国家之一.目前,某市就节水问题,召开了市民听证
会,并对水价进行激烈讨论,会后拟定方案如下:以户为单位,按月收缴,水价按照每户每
月用水量分三级管理,第一级为每月用水量不超过12吨,每吨3.5元;第二级计量范围为
超过12吨不超过18吨部分,第三级计量范围为超出18吨的部分,一、二、三级水价的单
价按1:3:5计价.
(1)请写出每月水费 (
( 元)与用水量
元)与用水量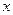 (吨)之间的函数关系;
(吨)之间的函数关系;
(2)某户居民当月交纳水费为63元,该户当月用水多少吨?
已知函数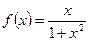 .
.
(1)证明函数具有奇偶性;
(2)证明函数在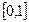 上是单调函数;
上是单调函数;
(3)求函数在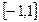 上的最值.
上的最值.
已知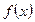 是二次函数,满足
是二次函数,满足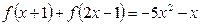 ,
, 求函数
求函数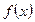 的
的
解析式、值域,并写出函数的单调递减区间.
已知集合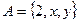 ,
,
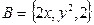 ,若
,若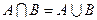 ,求实数
,求实数 、
、 的
的
值 .
.