已知函数 ,(
,( ).
).
(1)若 有最值,求实数
有最值,求实数 的取值范围;
的取值范围;
(2)当 时,若存在
时,若存在 、
、
 ,使得曲线
,使得曲线 在
在 与
与 处的切线互相平行,求证:
处的切线互相平行,求证: .
.
已知数列 的前n项和为
的前n项和为 满足:
满足: .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)令 ,对任意
,对任意 ,是否存在正整数m,使
,是否存在正整数m,使 都成立?若存在,求出m的值;若不存在,请说明理由.
都成立?若存在,求出m的值;若不存在,请说明理由.
某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.
设平面向量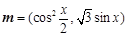 ,
, ,函数
,函数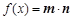 .
.
(1)当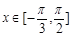 时,求函数
时,求函数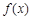 的取值范围;
的取值范围;
(2)当 ,且
,且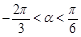 时,求
时,求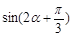 的值.
的值.
已知函数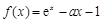 (
(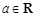 ).
).
(1)求函数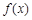 的单调区间;
的单调区间;
(2)函数 在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(3)若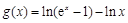 ,当
,当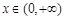 时,不等式
时,不等式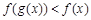 恒成立,求a的取值范围.
恒成立,求a的取值范围.
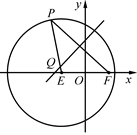
如图,已知圆E: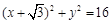 ,点
,点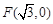 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹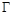 的方程;
的方程;
(2)已知A,B,C是轨迹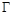 的三个动点,A与B关于原点对称,且
的三个动点,A与B关于原点对称,且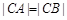 ,问△ABC的面积是否存在最小值?若存在,求出此时点C的坐标,若不存在,请说明理由.
,问△ABC的面积是否存在最小值?若存在,求出此时点C的坐标,若不存在,请说明理由.