如图1,在直角梯形 中,
中, ,
, ,
, ,点
,点 为
为 中点.将
中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(1)在 上找一点
上找一点 ,使
,使 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,问当a、b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?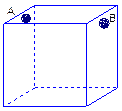
某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律 每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足R(x)=
每生产产品x(百台),其总成本为G(x)万元,其中固定成本为2万元,并且每生产100台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)满足R(x)=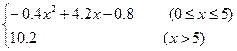 .假定该产品销售平衡,那么根据上述统计规律.
.假定该产品销售平衡,那么根据上述统计规律.
(1)要使工厂有盈利,产品x应控制在什么范围?
(2)工厂生产多少台产品时赢利最大?并求此时每台产品的售价为多少?
某城市2009年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相等. 为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
已知函数 在
在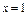 处取得极值。
处取得极值。
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数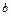 的取值范围;
的取值范围;
(3)证明: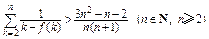 。参考数据:
。参考数据: 。
。
已知数列 满足
满足 ,且
,且 。
。
(1)证明:数列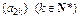 为等比数列;(2)求数列
为等比数列;(2)求数列 的通项公式;
的通项公式;
(3)设 为非零常数)。试确定
为非零常数)。试确定 的值,使得对任意
的值,使得对任意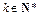 都有
都有 成立。
成立。