某校举行中学生“日常生活小常识”知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答一题的方式进行;每位选手最多有5次答题机会,选手累计答对3题或答错3题即终止比赛,答对3题者直接进入复赛,答错3题者则被淘汰.已知选手甲答对每个题的概率均为 ,且相互间没有影响.
,且相互间没有影响.
(1)求选手甲进入复赛的概率;
(2)设选手甲在初赛中答题的个数为 ,试求
,试求 的分布列和数学期望.
的分布列和数学期望.
已知 是一个等差数列,且
是一个等差数列,且 ,
,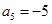 .(Ⅰ)求
.(Ⅰ)求 的通项
的通项 ;
;
(Ⅱ)求 前
前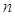 项和
项和 的最大值.
的最大值.
设 的内角
的内角 的对边分别为
的对边分别为 .已知
.已知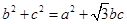 ,求:
,求:
(Ⅰ)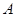 的大小;
的大小;
(Ⅱ)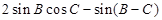 的值.
的值.
设椭圆E:  (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N(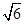 ,1)两点,O为坐标原点,(I)求椭圆E的方程;
,1)两点,O为坐标原点,(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
.某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 |
初二年级 |
初三年级 |
|
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知y 245,z
245,z 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
给定抛物线C:y2=4x,F是C的焦点,过点F的直线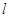 与C相交于A、B两点。
与C相交于A、B两点。
(1)设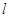 的斜率为1,求
的斜率为1,求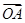 与
与 夹角的余弦值;
夹角的余弦值;
(2)设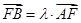 ,若
,若 ∈[4,9],求
∈[4,9],求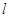 在y轴上截距的变化范围。
在y轴上截距的变化范围。