以直角坐标系的原点为极点O,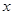 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.问:点B在什么位置时,四边形OACB面积最大?
已知直线L:kx-y+1+2k=0.
(1)求证:直线L过定点;
(2)若直线L交x轴负半轴于点A,交y正半轴于点B,△AOB的面积为S,试求S的最小值并求出此时直线L的方程.
△ABC中,a、b、c分别是角A、B、C的对边,△ABC的周长为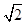 +2,且sinA+sinB=
+2,且sinA+sinB=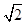 sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为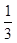 sinC,求角C的度数.
sinC,求角C的度数.
数列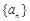 满足
满足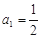 ,
,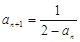
 .
.
(1)求证: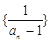 为等差数列,并求出
为等差数列,并求出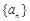 的通项公式;
的通项公式;
(2)设 ,数列
,数列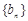 的前
的前 项和为
项和为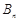 ,对任意
,对任意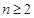 都有
都有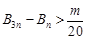 成立,求整数
成立,求整数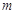 的最大值.
的最大值.
已知数列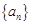 的前
的前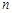 项和为
项和为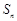 ,
,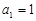 ,
, 是
是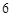 与
与 的等差中项(
的等差中项(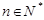 ).
).
(1)求数列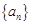 的通项公式;
的通项公式;
(2)是否存在正整数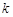 ,使不等式
,使不等式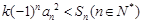 恒成立,若存在,求出
恒成立,若存在,求出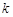
的最大值;若不存在,请说明理由.