如图，A地到火车站共有两条路径L1和L2，据统计，通过两条路径所用的时间互不影响，所用时间落在各时间段内的频率如下表：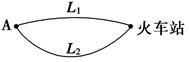
| 时间(分钟) |
10～20 |
20～30 |
30～40 |
40～50 |
50～60 |
| L1的频率 |
0.1 |
0.2 |
0.3 |
0.2 |
0.2 |
| L2的频率 |
0 |
0.1 |
0.4 |
0.4 |
0.1 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站．
(1)为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
(2)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数，针地(1)的选择方案，求X的分布列和数学期望．
如图扇形AOB是一个观光区的平面示意图，其中∠AOB的圆心角为
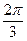，半径OA为1Km，为了便于游客观光休闲，拟在观光区内铺设一条从入口A到出口B的观光道路，道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上，且CD//AO，设∠AOC=θ，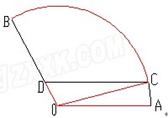
（1）用θ表示CD的长度，并写出θ的取值范围。
（2）当θ为何值时，观光道路最长？
如图, 椭圆C：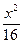
+
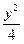=1的右顶点是A，上下两个顶点分别为B、D，四边形DAMB是矩形（O为坐标原点）
，点E、P分别是线段OA、AM的中点。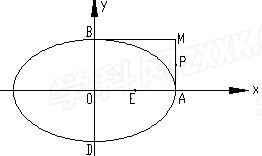
（1）求证：直线DE与直线BP的交点在椭圆C上.
（2）过点B的直线l1、l2与椭圆C分别交于R、S（不同于B点），且它们的斜率k1、k2满足k1*k2=-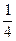
，求证：直线RS过定点，并求出此定点的坐标。
如图：四棱锥P-ABCD的底面为矩形，且AB=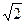
BC，E、F分别为棱AB、PC的中点。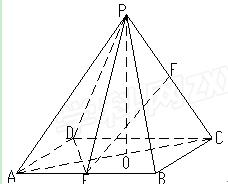
（1）求证：EF//平面PAD；
（2）若点P在平面ABCD内的正投影O在直线AC上，求证：平面PAC⊥平面PDE
已知向量a=（4，5cosσ），b=（3，-4tanσ），
（1）若a//b，试求sinσ的值。
（2）若a⊥b，且σ∈（0，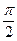
），求cos（2σ-
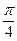）的值
（（本小题满分12分）
已知圆C：x2+(y－1)2 =5，直线l：mx－y+l－m=0，
（1）求证：对任意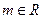
，直线l与圆C总有两个不同的交点。
（2）设l与圆C交于A、B两点，若| AB | =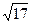 
，求l的倾斜角；
（3）求弦AB的中点M的轨迹方程；