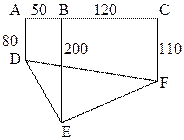某商场为促销设计了一个抽奖模型,一定数额的消费可以获得一张抽奖券,每张抽奖券可以从一个装有大小相同的4个白球和2个红球的口袋中一次性摸出3个球,至少摸到一个红球则中奖.
(1)求一次抽奖中奖的概率;
(2)若每次中奖可获得10元的奖金,一位顾客获得两张抽奖券,求两次抽奖所得的奖金额之和X(元)的概率分布.
已知函数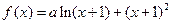 在
在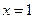 处有极值.
处有极值.
(Ⅰ)求实数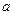 值;
值;
(Ⅱ)求函数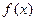 的单调区间;
的单调区间;
(Ⅲ)令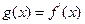 ,若曲线
,若曲线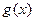 在
在 处的切线与两坐标轴分别交于
处的切线与两坐标轴分别交于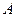 ,
,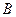 两点(
两点(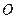 为坐标原点),求
为坐标原点),求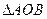 的面积.
的面积.
(10分) 设函数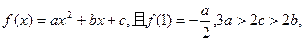 求证:
求证:
(1)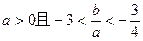 ;
;
(2)函数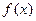 在区间(0,2)内至少有一个零点;
在区间(0,2)内至少有一个零点;
函数f(x)=是定义在(-1,1)上的奇函数,且f=.
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在(-1,1)上是增函数;
(3)解不等式f(t-1)+f(t)<0.
设数列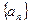 的前
的前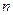 项和为
项和为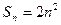 ,数列
,数列 为等比数列,且
为等比数列,且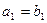 ,
,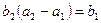 。(1)求数列
。(1)求数列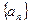 和
和 的通项公式;(2)设
的通项公式;(2)设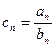 ,求数列
,求数列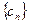 的前
的前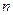 项和
项和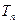 。
。
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量。已知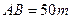 ,
, ,于
,于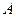 处测得水深
处测得水深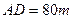 ,于
,于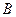 处测得水深
处测得水深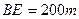 ,于
,于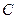 处测得水深
处测得水深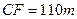 ,求
,求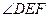 的余弦值。
的余弦值。