如图甲,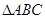 是边长为6的等边三角形,
是边长为6的等边三角形,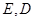 分别为
分别为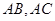 靠近
靠近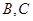 的三等分点,点
的三等分点,点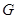 为边
为边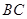 边的中点,线段
边的中点,线段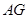 交线段
交线段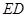 于点
于点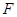 .将
.将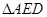 沿
沿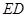 翻折,使平面
翻折,使平面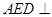 平面
平面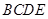 ,连接
,连接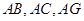 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.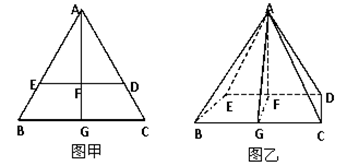
(1)求证: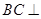 平面
平面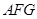
(2)求四棱锥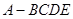 的体积.
的体积.
一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为 ,记
,记 .
.
(1)分别求出 取得最大值和最小值时的概率;(2)求
取得最大值和最小值时的概率;(2)求 的分布列及数学期望.
的分布列及数学期望.
已知数列 的前
的前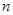 项和为
项和为 ,满足
,满足 .
.
(1)求 ;
;
(2)令 ,求数列
,求数列 的前
的前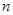 项和
项和 .
.
(3)设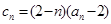 ,若对任意的正整数
,若对任意的正整数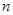 ,均有
,均有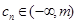 ,求实数
,求实数 的取值范围.
的取值范围.
已知△ABC中,角A、B、C的对边为a,b,c,向量

 =
= ,且
,且 . (1)求角C; (2)若
. (1)求角C; (2)若 ,试求
,试求 的值.
的值.
已知函数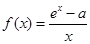 ,
, .
.
① 时,求
时,求 的单调区间;
的单调区间;
②若 时,函数
时,函数 的图象总在函数
的图象总在函数 的图象的上方,求实数
的图象的上方,求实数 的取值范围.
的取值范围.
抛物线 的焦点为
的焦点为 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点.
两点.
①若 ,求直线
,求直线 的斜率;
的斜率;
②设点 在线段
在线段 上运动,原点
上运动,原点 关于点
关于点 的对称点为
的对称点为 ,求四边形
,求四边形 面积的最小值.
面积的最小值.