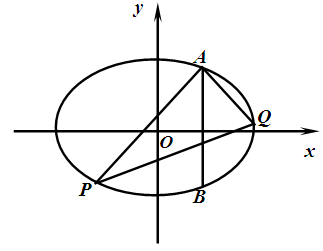
如图,两条相交线段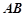 、
、 的四个端点都在椭圆
的四个端点都在椭圆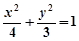 上,其中,直线
上,其中,直线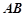 的方程为
的方程为 ,直线
,直线 的方程为
的方程为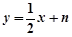 .
.
(1)若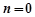 ,
,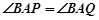 ,求
,求 的值;
的值;
(2)探究:是否存在常数 ,当
,当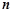 变化时,恒有
变化时,恒有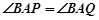 ?
?
本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知复数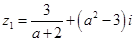 ,
,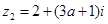 (
( ,
,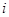 是虚数单位)。
是虚数单位)。
(1)若复数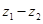 在复平面上对应点落在第一象限,求实数
在复平面上对应点落在第一象限,求实数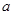 的取值范围
的取值范围
(2)若虚数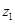 是实系数一元二次方程
是实系数一元二次方程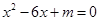 的根,求实数
的根,求实数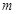 的值.
的值.
、(本小题满分14分)
已知函数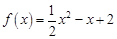 ,数列
,数列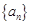 满足递推关系式:
满足递推关系式: (
(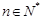 ),且
),且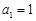 、
、
(Ⅰ)求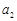 、
、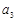 、
、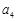 的值;
的值;
(Ⅱ)用数学归纳法证明:当 时,
时,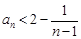 ;
;
(Ⅲ)证明:当 时,有
时,有 、
、
(本小题满分13分)
已知函数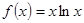 、
、
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若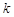 为正常数,设
为正常数,设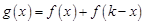 ,求函数
,求函数 的最小值;
的最小值;
(Ⅲ)若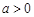 ,
,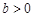 ,证明:
,证明: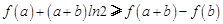 、
、
(本小题满分12分)
一个口袋中装有大小相同的 个红球(
个红球( 且
且 )和
)和 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
(Ⅰ)试用 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率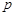 ;
;
(Ⅱ)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为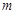 ,求
,求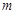 的最大值?
的最大值?
(Ⅲ)在(Ⅱ)的条件下,将 个白球全部取出后,对剩下的
个白球全部取出后,对剩下的 个红球全部作如下标记:记上
个红球全部作如下标记:记上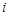 号的有
号的有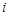 个(
个(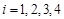 ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。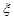 表示所取球的标号,求
表示所取球的标号,求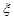 的分布列、期望和方差。
的分布列、期望和方差。
(本小题满分12分)
如图,已知 是直角梯形,
是直角梯形, ,
,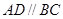 ,
, ,
,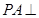 平面
平面 .
.
(1) 证明: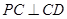 ;
;
(2) 若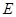 是
是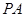 的中点,证明:
的中点,证明: ∥平面
∥平面 ;
;
(3)若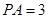 ,求三棱锥
,求三棱锥 的体积.
的体积.