设袋子中装有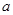 个红球,
个红球,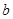 个黄球,
个黄球,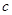 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当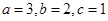 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量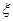 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求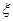 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量 为取出此球所得分数.若
为取出此球所得分数.若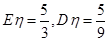 ,求
,求
设全集为R,集合 ,
,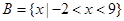 .
.
(1)求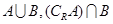 ;
;
(2)已知 ,若
,若 ,求实数
,求实数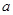 的取值范围.
的取值范围.
设数列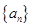 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,
,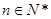 .
.
(1)求数列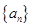 的通项公式;
的通项公式;
(2)证明:对一切正整数 ,有
,有 .
.
(本小题满分13分)已知椭圆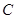 :
: (
( )的焦距为
)的焦距为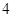 ,且过点
,且过点 .
.
(1)求椭圆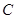 的方程和离心率;
的方程和离心率;
(2)设 (
( )为椭圆
)为椭圆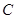 上一点,过点
上一点,过点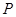 作
作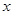 轴的垂线,垂足为
轴的垂线,垂足为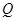 .取点
.取点 ,连 结
,连 结 ,过点
,过点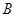 作
作 的垂线交
的垂线交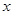 轴于点
轴于点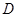 ,点
,点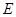 是点
是点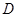 关于
关于 轴的对称点.试判断直线
轴的对称点.试判断直线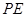 与椭圆
与椭圆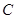 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(本小题满分13分)已知函数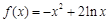 .
.
(1)求函数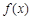 的最大值;
的最大值;
(2)若函数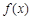 与
与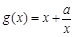 有相同极值点,
有相同极值点,
(ⅰ)求实数 的值;
的值;
(ⅱ)若对于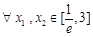 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本题满分12分)如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= CD=1,PD=
CD=1,PD=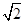 .
.
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PA与平面PBC所成角的正弦值;
(3)在线段PC上是否存在一点Q(除去端点),使得平面QAD与平面PBC所成锐二面角的大小为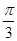 ?
?