一汽车厂生产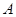 、
、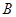 、
、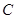 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| |
轿车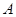 |
轿车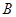 |
轿车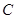 |
| 舒适型 |
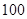 |
 |
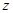 |
| 标准型 |
 |
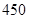 |
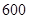 |
按类型分层抽样的方法在这个月生产的轿车中抽取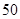 辆,其中有
辆,其中有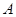 类轿车
类轿车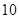 辆.
辆.
(1)求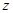 的值;
的值;
(2)用分层抽样的方法在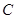 类轿车中抽取一个容量为
类轿车中抽取一个容量为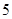 的样本.将该样本看成一个总体,从中任取
的样本.将该样本看成一个总体,从中任取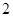 辆,求至少有
辆,求至少有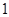 辆舒适型轿车的概率;
辆舒适型轿车的概率;
(3)用随机抽样的方法从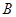 类舒适型轿车中抽取
类舒适型轿车中抽取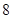 辆,经检测它们的得分如下:
辆,经检测它们的得分如下: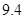 、
、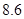 、
、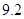 、
、 、
、 、
、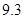 、
、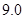 、
、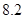 .把这
.把这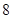 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
不超过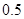 的概率.
的概率.
一矩形铁皮的长为8 cm,宽为5 cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大?
设命题p:(4x-3)2≤1;命题q:x2-(2a+1)x+a(a+1)≤0,若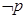 是
是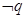 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.
已知函数
(1)当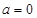 时,求
时,求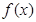 的最小值;
的最小值;
(2)在区间(1,2)内任取两个实数p,q,且p≠q,若不等式 >1恒成立,求实数a的取值范围;
>1恒成立,求实数a的取值范围;
(3)求证: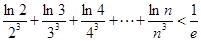 (其中
(其中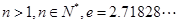 )。
)。
已知椭圆 :
:
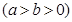 的离心率
的离心率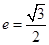 ,原点到过点
,原点到过点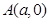 ,
,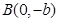 的直线的距离是
的直线的距离是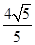 .
.
(1)求椭圆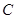 的方程;
的方程;
(2)若椭圆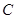 上一动点
上一动点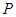
 关于直线
关于直线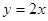 的对称点为
的对称点为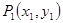 ,求
,求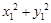 的取值范围;
的取值范围;
(3)如果直线 交椭圆
交椭圆 于不同的两点
于不同的两点 ,
,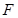 ,且
,且 ,
,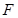 都在以
都在以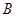 为圆心的圆上,求
为圆心的圆上,求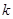 的值.
的值.
如图,在直三棱柱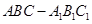 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中, ,
, ,
,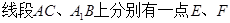 ,且满足
,且满足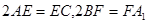 .
.
(1)求证:平面 侧面
侧面 ;
;
(2)求二面角 的平面角的余弦值。
的平面角的余弦值。