小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从 ,
, (如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(如图)这8个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为X。若X=0就参加学校合唱团,否则就参加学校排球队。
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
(本小题满分14分)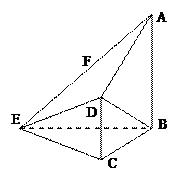 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
AB=BC=CE=2CD=2,∠BCE=1200,F为AE中点。
(Ⅰ) 求证:平面ADE⊥平面ABE ;
(Ⅱ)求二面角A—EB—D的大小的余弦值;
(Ⅲ)求点F到平面BDE的距离。
(本小题满分14分)已知数列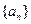 的首项
的首项 ,
, ,
,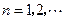 .
.
(Ⅰ)求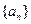 的通项公式;(Ⅱ)证明:对任意的
的通项公式;(Ⅱ)证明:对任意的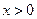 ,
,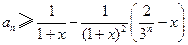 ,
,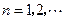 ;(Ⅲ)证明:
;(Ⅲ)证明: .
.
(本小题满分14分)如图,已知直线l: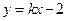 与抛物线C:
与抛物线C: 交于A,B两点,
交于A,B两点, 为坐标原点,
为坐标原点,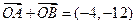 。
。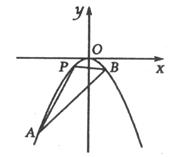
(Ⅰ)求直线l和抛物线C的方程;(Ⅱ)抛物线上一动点P从A到B运动时,求△ABP面积最大值.
(本小题满分12分)已知关于 的一元二次函数
的一元二次函数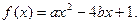 (Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
(Ⅰ)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为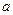 和
和 ,求函数
,求函数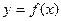 在区间[
在区间[ 上是增函数的概率;(Ⅱ)设点(
上是增函数的概率;(Ⅱ)设点(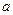 ,
, )是区域
)是区域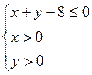 内的随机点,求函数
内的随机点,求函数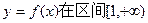 上是增函数的概率。
上是增函数的概率。
(本小题满分13分)已知函数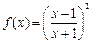 (其中x≥1且x≠2).
(其中x≥1且x≠2).
(1)求函数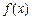 的反函数
的反函数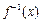
(2)设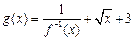 ,求函数
,求函数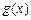 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式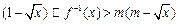 对于区间
对于区间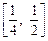 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.